Le rôle des analogies dans la résolution de problèmes aux cycles 2 et 3
Emmanuel SanderEmmanuel SANDER : https://www.unige.ch/fapse/idea/fr/equipe/sander/ est Professeur à l’Université de Genève, en psychologie. L’orientation générale de ses recherches s’inscrit dans une perspective cognitive et développementale en lien avec les questions de l’éducation. Ses problématiques concernent la mise en évidence et l’analyse du rôle des connaissances préalables dans les activités de compréhension et de raisonnement à travers des situations d’acquisition de connaissances.
| player1 | |
| 1- Les connaissances du quotidien et les connaissances mathématiques interagissent en résolution de problèmes | 00:00:00 |
| 2- Comparaison de 2 problèmes relevant des mêmes concepts mathématiques mais de difficultés très différentes | 00:04:04 |
| 3- Lorsque les connaissances du quotidien font obstacle au traitement mathématique de la situation : Le recodage sémantique | 00:11:44 |
| 4- Les analogies intuitives | 00:15:06 |
| 5- Trois formes d’analogies intuitives, facilitatrices ou obstructives | 00:18:50 |
| 6- Les analogies de substitution | 00:23:42 |
| 7- Les analogies de scénario | 00:34:54 |
| 8- Exemples pour distinguer analogies de substitution et analogies de scénario | 00:39:00 |
| 9- Les analogies de simulation | 00:41:00 |
Les connaissances du quotidien et les connaissances mathématiques interagissent en résolution de problèmes
 En situation de résolution de problèmes arithmétiques, les élèves travaillent à la fois la cognition mathématique et la cognition langagière. C’est-à-dire qu’en résolution de problèmes, interviennent des aspects extra-mathématiques, qui vont permettre aux élèves de se construire une représentation mathématique des problèmes, qui reposent sur le langage. Cette intrication des aspects mathématiques et langagiers ne représente pas nécessairement un obstacle à la résolution. Un problème va évoquer des concepts qui relèvent de connaissances liées à la vie quotidienne de l’élève sur lesquelles il pourra s’appuyer pour construire une représentation mathématique du problème et donc des connaissances mathématiques.
En situation de résolution de problèmes arithmétiques, les élèves travaillent à la fois la cognition mathématique et la cognition langagière. C’est-à-dire qu’en résolution de problèmes, interviennent des aspects extra-mathématiques, qui vont permettre aux élèves de se construire une représentation mathématique des problèmes, qui reposent sur le langage. Cette intrication des aspects mathématiques et langagiers ne représente pas nécessairement un obstacle à la résolution. Un problème va évoquer des concepts qui relèvent de connaissances liées à la vie quotidienne de l’élève sur lesquelles il pourra s’appuyer pour construire une représentation mathématique du problème et donc des connaissances mathématiques.
En ce sens, au cycle 2, la résolution de problèmes peut représenter un appui pour construire le sens des opérations.
Comparaison de 2 problèmes relevant des mêmes concepts mathématiques mais de difficultés très différentes
Sur le plan des connaissances du quotidien, les deux problèmes ci-dessous font appel à des connaissances extra-mathématiques différentes :
- Les oiseaux, les vers
- Les oiseaux peuvent manger les vers
- À l’école les partages sont généralement équitables
- Etc.

Le deuxième énoncé représente une moindre difficulté de résolution parce que les élèves peuvent se construire une représentation mentale du scénario en réalisant une mise en correspondance. En CP, 96% des élèves résolvent correctement le deuxième problème tandis que seulement 25% réussissent le premier.
On est donc en présence de deux énoncés de problèmes qui relèvent des mêmes connaissances mathématiques mais pas des mêmes connaissances extra-mathématiques. Pour le problème 2, on est même en mesure de s’interroger pour savoir si les connaissances du quotidien n’occultent pas le traitement mathématique de la situation. Est-ce que l’élève fait des mathématiques lorsqu’il traite mentalement d’une situation d’ajout/retraitJean-Jacques Calmelet explique la différence entre une situation d'addition/soustraction et une situation d'ajout/retrait lors de la conférence de consensus du CNESCO "Nombres et Calculs au Primaire" qui s'est tenue en novembre 2015 - http://www.cnesco.fr/fr/numeration/paroles-dexperts/conferences-introductives/
Lorsque les connaissances du quotidien font obstacle au traitement mathématique de la situation : Le recodage sémantique
Un même énoncé peut faire l’objet de lectures/interprétations de natures différentes. Quand on est enseignant et qu’on constate que les élèves mobilisent des stratégies de résolution inadaptées liées à des mésinterprétations du texte d’énoncé, comment aider les élèves pour favoriser une compréhension arithmétique du problème et la mobilisation des notions mathématiques adaptées ?
Comparer des problèmes dont les scénarios sont proches et qui relèvent des mêmes opérations pour analyser les relations sémantiques de ces énoncés, les ruptures et les continuités dans la compréhension du texte et la compréhension arithmétique de la situation, permet de repérer les notions mathématiques incarnées par ces énoncés.
Le recodage sémantique, conduit par l’enseignant, consiste à faire avancer la compréhension d’un élève en allant à l’encontre de son intuition. Parfois des éléments de la situation orientent vers une certaine conception mathématique, mais celle-ci n’est pas adaptée au problème. Le recodage sémantique va initier une autre façon de percevoir le problème, qui, elle, est cohérente avec les objectifs mathématiques visés.
Les analogies intuitives
Si on admet que toute connaissance nouvelle est appréhendée à partir de connaissances préalables, les analogies intuitives sont les manières dont spontanément, lorsqu’une notion est introduite, on va l’appréhender. Face à la nouveauté, l’élève va s’appuyer sur ce qui est connu. Les analogies intuitives ont donc une valeur adaptative très importante et très pertinente puisqu’à l’école les connaissances nouvelles reposent généralement sur des connaissances préalables
S’appuyer sur les analogies intuitives et non intuitives pour orienter le développement conceptuel
À partir du moment où un élève a une conception première d’une situation scolaire qui lui a permis d’entrer et de structurer une notion scolaire, celle-ci appartient à son répertoire d’analogies intuitives. Pour l’enseignant reconnaissant cette conception, se pose la question de comment la faire évoluer et favoriser son développement ? C’est là qu’intervient le recodage sémantique. L’enseignant va travailler avec l’élève sur des analogies non intuitives qui, elles, vont favoriser une décontextualisation et une montée en abstraction orientée par la pertinence mathématique.
Trois formes d’analogies intuitives, facilitatrices ou obstructives
 Les travaux de recherche d’Emmanuel Sander et son équipe les ont conduits à concevoir un cadre théorique : le cadre A-S3 (Analogies intuitives de Substitution, de Scénario et de Simulation). Les outils construits par ACERecherche ACE, Arithmétique et Compréhension à l'École élémentaire : http://blog.espe-bretagne.fr/ace/ s’inscrivent dans ce cadre théorique qui différencie trois formes d’analogies intuitives : les analogies de substitution, de scénario et de simulation. Dans la mesure où elles agissent parfois de manière facilitatrice et parfois de manière obstructive, il est utile de savoir comment les problèmes proposés se situent au regard de ces trois formes d’analogies pour en anticiper les effets et prendre en charge les questions qui en découlent :
Les travaux de recherche d’Emmanuel Sander et son équipe les ont conduits à concevoir un cadre théorique : le cadre A-S3 (Analogies intuitives de Substitution, de Scénario et de Simulation). Les outils construits par ACERecherche ACE, Arithmétique et Compréhension à l'École élémentaire : http://blog.espe-bretagne.fr/ace/ s’inscrivent dans ce cadre théorique qui différencie trois formes d’analogies intuitives : les analogies de substitution, de scénario et de simulation. Dans la mesure où elles agissent parfois de manière facilitatrice et parfois de manière obstructive, il est utile de savoir comment les problèmes proposés se situent au regard de ces trois formes d’analogies pour en anticiper les effets et prendre en charge les questions qui en découlent :
- Si l’analogie intuitive facilite la résolution, et que l’élève réussit, il a peut-être traité la situation sans mobiliser les connaissances mathématiques souhaitées. La question est alors de savoir s’il aurait réussi sans l’effet facilitateur.
- Si l’analogie agit plutôt de façon obstructive et que l’élève échoue dans la résolution, comment l’aider à dépasser ces analogies intuitives ?
L’expérience montre qu’il y a interdépendance entre ces trois formes d’analogies mais qu’il est possible de les dissocier. Elles peuvent représenter un véritable levier au service des apprentissages dans la mesure où elles peuvent servir à :
- Se prononcer sur la difficulté d’un problème pour prédire les difficultés que les élèves pourront rencontrer.
- Analyser les performances des élèves en distinguant dans les résolutions réussies si elles reposent sur une expertise facilitée par les analogies intuitives ou si elles relèvent d’une compréhension plus profonde des notions mathématiques.
- Concevoir des évaluations en cohérence avec les situations enseignées.
- Planifier son enseignement en prenant en compte les analogies intuitives pour concevoir une progression des apprentissages mathématiques.
- Travailler en formation.
Les analogies de substitution
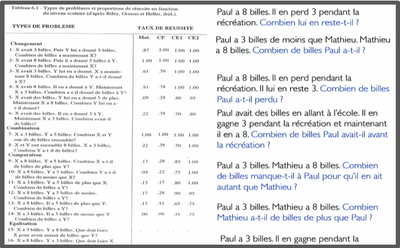 Les analogies de substitution désignent le fait que la notion mathématique est perçue par analogie avec une connaissance familière issue de la vie quotidienne. Le langage ordinaire porte en lui ces analogies de substitution. Par exemple si on se réfère aux définitions extra-mathématiques de « soustraction » données par les dictionnaires, on trouve l’idée de « retirer », « d’enlever », « de perdre ». Or ce sens extra-mathématique ne recouvre que partiellement la notion mathématique de soustraction. C’est-à-dire que parmi les situations mathématiques relevant de la soustraction, seules quelques-unes sont incarnées par des problèmes relevant de situations de pertes. Si on se réfère à la typologie de Gérard Vergnaud, il recense 11 catégories de problèmes relevant de la soustraction et seulement 1 correspondant à l’analogie de substitution. Concrètement cela peut signifier qu'en présence de 11 problèmes arithmétiques différents relevant de la soustraction, un élève n’en traitera qu’un seul en utilisant une soustraction. Il aura, dans ce cas, mobilisé la connaissance du quotidien « une soustraction correspond à une situation de perte » car il s'agit pour lui de rechercher le résultat d'une perte. Les 10 autres problèmes ne traitant pas de ce type de situation, ils sont hors du domaine de validité de l’analogie de substitution de la soustraction. L'élève les traitera autrement. Leur reconnaissance comme problèmes relevant de la soustraction nécessitera un enseignement spécifique passant par une analyse sémantique du texte d’énoncé et un recodage sémantique nécessitant l'enseignement d'analogies non-intuitives.
Les analogies de substitution désignent le fait que la notion mathématique est perçue par analogie avec une connaissance familière issue de la vie quotidienne. Le langage ordinaire porte en lui ces analogies de substitution. Par exemple si on se réfère aux définitions extra-mathématiques de « soustraction » données par les dictionnaires, on trouve l’idée de « retirer », « d’enlever », « de perdre ». Or ce sens extra-mathématique ne recouvre que partiellement la notion mathématique de soustraction. C’est-à-dire que parmi les situations mathématiques relevant de la soustraction, seules quelques-unes sont incarnées par des problèmes relevant de situations de pertes. Si on se réfère à la typologie de Gérard Vergnaud, il recense 11 catégories de problèmes relevant de la soustraction et seulement 1 correspondant à l’analogie de substitution. Concrètement cela peut signifier qu'en présence de 11 problèmes arithmétiques différents relevant de la soustraction, un élève n’en traitera qu’un seul en utilisant une soustraction. Il aura, dans ce cas, mobilisé la connaissance du quotidien « une soustraction correspond à une situation de perte » car il s'agit pour lui de rechercher le résultat d'une perte. Les 10 autres problèmes ne traitant pas de ce type de situation, ils sont hors du domaine de validité de l’analogie de substitution de la soustraction. L'élève les traitera autrement. Leur reconnaissance comme problèmes relevant de la soustraction nécessitera un enseignement spécifique passant par une analyse sémantique du texte d’énoncé et un recodage sémantique nécessitant l'enseignement d'analogies non-intuitives. Les analogies de substitution sont robustes et elles opèrent spontanément chez tout un chacun. Si on demande à un expert des mathématiques de produire un énoncé de problème arithmétique relevant de la soustraction, il produira spontanément un énoncé appartenant au domaine de validité de l’analogie de substitution, c’est-à-dire un énoncé traitant d’une situation de perte. Il est donc inutile de lutter contre les effets liés à ces analogies, il s'agit plutôt de les anticiper et de confronter régulièrement les élèves à des situations dans lesquelles elles n'opèrent pas pour d'analyser avec eux les contextes sémantiques d'énoncés de problèmes relevant de la soustraction.
Les analogies de substitution sont robustes et elles opèrent spontanément chez tout un chacun. Si on demande à un expert des mathématiques de produire un énoncé de problème arithmétique relevant de la soustraction, il produira spontanément un énoncé appartenant au domaine de validité de l’analogie de substitution, c’est-à-dire un énoncé traitant d’une situation de perte. Il est donc inutile de lutter contre les effets liés à ces analogies, il s'agit plutôt de les anticiper et de confronter régulièrement les élèves à des situations dans lesquelles elles n'opèrent pas pour d'analyser avec eux les contextes sémantiques d'énoncés de problèmes relevant de la soustraction.
Les analogies de scénario
Les analogies de scénario ont à voir avec les scénarios évoqués par les situations des problèmes. Parfois, les objets présents dans les situations invitent à des scénarios qui sont plus ou moins compatibles avec certaines opérations mathématiques. Par exemple, un problème dans lequel les objets sont « 12 oranges » et « 4 pommes » va spontanément évoquer la collection des « fruits » dans les connaissances du quotidien et orienter vers l’opération mathématique de l’addition. Tandis que si dans le problème il est question de « 12 oranges » et de « 4 paniers », les données numériques sont les mêmes : 12 et 4, mais les connaissances du quotidien vont plutôt orienter vers une répartition équitable des oranges dans les paniers et donc vers une division. Selon les connaissances qu’on a des relations fonctionnelles entre les objets cités dans les énoncés mathématiques, il est difficile d’envisager que ces objets incarnent certaines opérations tant les scénarios du quotidien sont robustes. Ainsi dans l’énoncé avec « 12 oranges » et « 4 pommes », la question « combien ai-je de fois de plus d’oranges que de pommes ? » va mettre en difficulté nombre d’élèves de cycle 3 car l’analogie de scénario joue un rôle obstructif, tandis que s’il s’agit des mêmes 12 oranges à ranger dans 4 paniers, le problème l’analogie de scénario jouera un rôle facilitateur du fait de la relation fonctionnelle existant entre les oranges et les paniers.
Exemples pour distinguer analogies de substitution et analogies de scénario
Dans ce chapitre, Emmanuel Sander propose trois énoncés de problèmes arithmétiques et les analyse sous l’angle des analogies de substitution et de scénario pour savoir si ces analogies fonctionnent plutôt de façon facilitatrice ou obstructive dans la résolution du problème.
Les analogies de Simulation
 L’analogie de simulation revient à simuler mentalement la situation décrite par l’énoncé. Elle peut agir de façon facilitatrice ou obstructive.
L’analogie de simulation revient à simuler mentalement la situation décrite par l’énoncé. Elle peut agir de façon facilitatrice ou obstructive.
Si on s’intéresse au premier problème, l’analogie de simulation va permettre de résoudre le problème par une procédure mentale de surcomptage (analogie facilitatrice) tandis que dans le second problème, la perte de 27 billes, nombre trop grand pour s’en construire une image mentale facile à manipuler, représente une analogie de simulation obstructive.
Revenir à l'ensemble des conférences sur les mathématiques (2018-2020) en cliquant sur cette icône





