COMMENT METTRE EN OEUVRE LE PRESCRIT DES PROGRAMMES?
| player1 | |
| Dans les programmes, les décimaux à l'intersection de trois domaines des mathématiques. | 00:00:00 |
| Le cas particulier de la multiplication de deux décimaux. | 00:02:57 |
| Continuité rupture entre manipulation et preuve. | 00:05:02 |
Dans les programmes, les décimaux à l'intersection de trois domaines mathématiques
Dans les programmes, trois domaines sont imbriqués:
- Nombres et Calculs
- Grandeurs et Mesures
- Espace et Géométrie.
Ce qui permet d'avancer en formation que les décimaux doivent être liés au travail sur les grandeurs. Concernant les calculs, le recours aux techniques opératoires ne doivent avoir lieu que lorsque le besoin s'en fait sentir. J. Briand revient ici sur la question des algorithmes évolutifs (Cf Conférence Place et rôle de la manipulation dans la construction du nombre et la résolution de problème aux cycles 1,2 et 3.).
Les décimaux se situent également dans ce cheminement. Avec ses élèves, l'enseignant s'est appliqué à construire la numération, il a abordé l'addition et la soustraction, a travaillé sur la droite numérique. Au détour du travail sur les grandeurs, les élèves s'aperçoivent que pour mesurer entre 3 et 4, il y a un creux qu'il faut combler. Au CM1, les décimaux arrivent lorsque les nombres entiers ne suffisent plus pour mesurer.
Le cas particulier de la multiplication de deux décimaux
L'étude de la multiplication de deux nombres décimaux entre et sort des programmes du 1er degré régulièrement. Actuellement, elle n'est pas présente car c'est un sujet complexe à étudier, il est donc dévolu au 2nd degré. C'est une véritable rupture avec la multiplication d'un nombre décimal par un nombre entier naturel qui n'est finalement que la concaténation de l'addition.
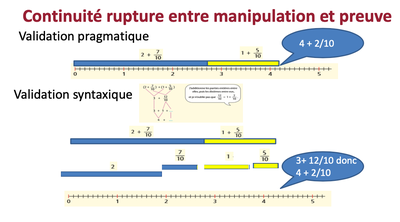
Continuité rupture entre manipulation et preuve
J. Briand propose de réfléchir à comment réfuter des conceptions erronées en 6ème. Il présente différents travaux d'enseignants.
1. Ce travail a pour objectif de montrer aux élèves que le modèle 1/2 + 2/5 = 3/7 est erroné par la mise bout à bout des bandes. Peut-être manque-t-il l'étape qui permet de montrer que les deux bandes accolées ne correspondent pas à 3/7, c'est-à-dire par le passage du partage de l'unité en 7.
2. Par contre dans l'exemple suivant, accoler les bandes sur une ligne graduée ne permet pas d'illustrer le résultat. On en reste à une validation pragmatique. En effet, cette démarche ne montre pas l'addition des dixièmes entre eux et des unités entre elles. La validation syntaxique, c'est-à-dire par le langage, induit une autre démarche. Il faut couper chacune des bandes en morceaux, en séparant unités et dixièmes, puis lors de la manipulation, accoler dans un premier temps les bandes-unités puis les bandes-dixièmes. J. Briand met en garde cependant. Cette démarche, par l'outil informatique, reste très ostensive.
Le passage de mise bout à bout des bandes à la décomposition en unités et dixièmes est une vrai rupture dans l'enseignement des additions de décimaux. Elle doit être anticipée. Le travail sur la droite numérique aide dans ce passage vers l'écriture chiffrée.
Revenir au dossier "Nombres décimaux: questions d'enseignement et de formation" en cliquant sur cette icône