DES SAVOIRS UTILES AU FORMATEUR POUR BIEN ACCOMPAGNER LES ENSEIGNANTS SUR LES DÉCIMAUX
| player1 | |
| Pourquoi s’intéresser aux décimaux | 00:00:00 |
| Plan et introduction | 00:04:47 |
| Place des savoirs dans les situations de classe | 00:06:04 |
| État des lieux dans l’enseignement des décimaux | 00:17:42 |
| Apports théoriques sur les décimaux | 00:25:32 |
Pourquoi s'intéresser aux décimaux?
Selon J. Briand, les enseignants des 1er et 2nd degrés ont des lacunes sur la question des nombres décimaux. Par ailleurs, l'institution donne régulièrement des consignes fluctuantes sur leur enseignement.
En formation, l'approche des décimaux serait plutôt didactique afin d'aborder le notion d'obstacle, de mettre en évidence des "points aveugles" dans cet enseignement (la droite numérique), de réfléchir sur les liens entre manipulation et conceptualisation et d'étudier au sein d'une relation école-collège le difficile passage de la fraction partage à la fraction quotient.
Plan et introduction
J. Briand base son propos sur la comparaison de situations. Il propose de faire un état des lieux et de s'intéresser aux questions que pose l'enseignement des décimaux.
En formation, il est intéressant de faire l'état des lieux des pratiques, puis d'étudier des manuels, regarder les effets sur les élèves. Ce n'est qu'après cette démarche réflexive qu'une progression sur les décimaux pourra être élaborée.
Place des savoirs dans les situations de classe
 La situation de classe proposée est l'introduction de la somme de deux décimaux en écriture à virgule. L'enseignant a introduit les écritures à virgule à partir de fractions décimales.
La situation de classe proposée est l'introduction de la somme de deux décimaux en écriture à virgule. L'enseignant a introduit les écritures à virgule à partir de fractions décimales.
Remarque: même en classe de 6ème cette situation pose problème. En effet, les élèves ne font pas toujours le lien entre le nombre décimal et le mesurage. Par exemple 1m25cm n'est pas compris comme étant la même mesure que 1,25m.
J. Briand présente quatre scénarios d'enseignement et propose de les étudier au travers du cadre de Chevallard en se basant sur quatre axes de réflexion :
- Y a-t-il un problème posé?
- Quelle est l'action de l'élève?
- Y a-t-il transfert de responsabilité vers l'élève?
- Quelle est la nature de la tâche?
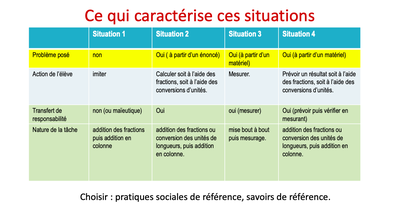 En formation, on peut demander quelle situation les participants choisiraient. Le but est de les amener notamment à distinguer les situations 3 et 4 concernant le rôle de la manipulation.
En formation, on peut demander quelle situation les participants choisiraient. Le but est de les amener notamment à distinguer les situations 3 et 4 concernant le rôle de la manipulation.
Que serait-il arrivé si l'enseignant avait choisi comme longueurs : 1,4 et 2,5 ? Il aurait obtenu une réussite fictive. En formation, cela permet d'aborder la notion de variables didactiques : données qui influent significativement sur le déroulement d'une séquence de classe.
Par ailleurs, il apparait important d'introduire la somme de deux décimaux par la manipulation afin que les élèves cernent à quoi cette opération correspond dans un milieu matériel.
Faire des maths c'est construire un modèle (produit par un langage) en vue d'exercer un contrôle sur un milieu. Il ne s'agirait pas de faire des élèves des "mesureurs". Ça consiste donc à résoudre des problèmes, anticiper, s'entrainer, apprendre et retenir. La présence d'un milieu matériel n'implique pas la réduction de l'activité à une simple manipulation. J. Briand alerte sur la verbalisation. Certains élèves sont capables de réaliser une tâche sans pour autant la verbaliser. Brousseau nommait cela la "théorie implicite d'action".
État des lieux dans l'enseignement des décimaux
Une formation sur les décimaux pourrait débuter par un état des lieux de cet enseignement. J. Briand dresse un rapide portrait par le biais d'outils qu'il utilise :
- un sondage demandant aux professeurs des écoles "Qu'est-ce qu'un nombre décimal?" permet de lancer le débat sur la définition de chacun sur les nombres décimaux;
- la comparaison de manuels scolaires et notamment le moment de l'introduction de l'écriture à virgule est révélateur de la démarche pédagogique sous-jacente;
- la représentation des ensembles des nombres en mathématiques crée un obstacle didactique en laissant croire que les ensembles sont emboités (c'est une représentation qui induit par exemple que les nombres naturels sont un ensemble connexe or entre deux nombres entiers il y a une infinité de nombres décimaux)
- une analyse des résultats des élèves lors d'un exercice de 6ème donne un aperçu des besoins et des pratiques antérieures. Si les enfants réussissent bien le pliage des bandes, ils échouent massivement sur l'écriture chiffrée. L'activité de pliage n'est pas opérationnelle.
Apports théoriques sur les décimaux
 Est-ce qu'avec les nombres décimaux et les fractions, on recouvre toute la droite numérique ? Autrement dit, est-ce que les décimaux c'est dense sur la droite? Non, il y a encore une infinité de trous.
Est-ce qu'avec les nombres décimaux et les fractions, on recouvre toute la droite numérique ? Autrement dit, est-ce que les décimaux c'est dense sur la droite? Non, il y a encore une infinité de trous.
En formation, cela peut être montré par le calcul de la longueur de la diagonale d'un carré de un centimètre de côté.
L'intérêt des décimaux est donc d'approcher, exprimer un ordre de grandeur, prolonger les règles de calcul sans que ce soit trop coûteux, et dans la classe éveiller la curiosité autour de l'exploration de la droite numérique.
Dans le cadre de situations-problèmes en classe, il est possible de montrer que certaines fractions ne renvoient pas à des nombres décimaux, comme dans l'exemple du dernier problème qui suit :
Le nombre décimal 4,33 n'est qu'une approximation.

- Pour aborder la question de l'ordre des nombres décimaux, J. Briand propose un exercice de classement de nombres comme on pourrait l'avoir dans un dictionnaire, c'est-à-dire en considérant les nombres comme des mots et donc les chiffres comme des lettres.
 Puis il propose d'ajouter 0,.. devant chaque nombre et de les classer du plus petit au plus grand. Il fait remarquer que l'ordre est le même, donc l'ordre de la partie décimale est un ordre lexicographique.
Puis il propose d'ajouter 0,.. devant chaque nombre et de les classer du plus petit au plus grand. Il fait remarquer que l'ordre est le même, donc l'ordre de la partie décimale est un ordre lexicographique.
En classe, l'erreur de l'élève qui indique que 1,2 et plus petit que 1,15 est fréquente. Nombre d'enseignants pense régler cet obstacle en changeant 1,2 par 1,20. Or, cela est un prolongement de l'ordre des entiers naturels. Le passage par l'ordre lexicographique peut être coûteux et périlleux mais il s'agit en formation de rendre les enseignants conscients de leur pratique.
Cependant, J. Briand alerte sur la perméabilité didactique. Certaines situations semblent fonctionner donc le formateur ou l'enseignant peuvent légitimement avoir envie de les tester dans leur milieu d'exercice. Mais il faut une solide formation didactique pour être en capacité de recevoir les travaux des élèves et de les traiter.
Revenir au dossier "Nombres décimaux: questions d'enseignement et de formation" en cliquant sur cette icône





