La manipulation en mathématiques
Objectifs de la formation
|
Concevoir des formations pour aider les enseignants à faire réussir tous les élèves
|
- Comprendre qu'on manipule pour penser et que la matérialité est au coeur des apprentissages
- Interroger les doxas sur la manipulation.
- Se mettre au clair sur les enjeux de la manipulation à partir d'apports de la recherche.
- Identifier les concepts-clés de "matérialité" ainsi que les ''objets déplaçables''/''objets non-déplaçables'', "les objets modifiables/objets non-modifiables"
Format : Enseignants en cycle 2 et cycle 3 idéalement, éventuellement en inter-degré 1x3H
Proposition de Déroulement
|
|
|
Description |
Ce que je gagne |
Ce que je perds |
|---|---|---|
|
Je manipule/je fais manipuler en classe pour... |
|
|
|
Je manipule/je fais manipuler en classe pour... |
|
|
 Propositions de traitement du visionnage des vidéos (temps 2 ) :
Propositions de traitement du visionnage des vidéos (temps 2 ) :
Avant de projeter les vidéos, il semble important que le formateur prenne connaissance des points de vigilance proposés dans le dossier ici, qu'il en dise quelques mots et qu'il contextualise la provenance de ces vidéos pour préparer les enseignants au travail qui va suivre.
Phase 1 : Description des faits observés le plus précisément possible du point de vue du maître et de l’élève, le formateur peut dire "Nous allons observer le travail de collègues qui ont acceptées d’être filmées. Il va s'agir d'un travail de comparaison entre des pratiques différentes. Dans un premier temps vous allez essayer de lister ce qui est plutôt pareil/plutôt différent, sans prêter d'intentions aux enseignantes lorsqu'elles font ce qu'elles font. A la fin du travail, nous pourrons écouter des extraits d’entretiens avec ces enseignantes, qui nous donneront des éléments sur leurs raisons d’agir"
Phase 2 : Postuler la cohérence de la pratique : L'objet de cette deuxième étape consiste à réfléchir et émettre des hypothèses sur les raisons pour lesquelles les enseignants font ce qu'ils font ? Cette deuxième étape permet de faire émerger des doxas, des principes, les systèmes de croyances et connaissances qui guident l'action des enseignants. Le formateur essaiera au maximum de les reformuler en tension, dilemmes, principes d'organisation des apprentissages autant que faire se peut. Il pourra, par exemple, dire : "Nous allons postuler la cohérence des pratiques observées; c'est à dire que nous allons partir du principe que ces enseignantes ont de bonnes raisons de faire ce qu'elles font comme elles le font.Nous allons donc formuler des hypothèses sur ce qui les conduit à agir comme elles le font".
Phase 3 : Identifier les intérêts et limites inhérents à toute pratique : le formateur peut souligner "Nous allons maintenant nous interroger sur les conflits de critères, les tensions, les problèmes de métiers et les dilemmes rencontrés par ces enseignantes. C'est à dire que nous n'allons pas essayer de déterminer si ce qu'elles font est "bien" ou pas, mais plutôt ce qu'elles gagnent et perdent à faire comme elles font. Pour cela nous allons nous poser la question pour chacune d'elle : en procédant comme elle l'a fait, qu'est-ce que l'enseignante a gagné ? Qu'est-ce qu'elle a perdu ?".
Phase 4 : Catégorisation à partir de l’analyse; trouver ensemble des alternatives adaptées aux contextes d'exercice des formés, utiles et efficaces.
A partir de la vidéo de Séverine chapitre 2 et la vidéo d'Ingrid Chapitre 1, 2 et 3. Le formateur peut proposer de compléter le tableau suivant
|
Description |
Ce qu'elle gagne/ce qu'elle perd ou Intérêts/limites |
Ce que les élèves gagnent/ce que les élèves perdent ou Intérêts/limites |
|---|---|---|
|
Les élèves de Séverine ou Séverine manipulent.... |
|
|
|
Les élèves d'Ingrid ou Ingrid manipulent.... |
|
|
Discussion et synthèse (temps 3 ) :
Ressources pour le formateur :
- Interview de Pierre Eysseric dans les cahiers pédagogiques
- Les concept-clés dans les premiers apprentissages de Claire Margolinas et Marceline Laparra
- Représenter, registres sémiotiques (Eduscol), (Raymond Duval)
- Modéliser, modéliser (Eduscol)
Résoudre un problème en se plaçant dans la peau d'un élève (temps 4 ) :
Le formateur peut proposer le problème suivant :
Une marchande de gaufres vend les 3/5 le matin. Elle vend un quart de ce qui lui reste l’après-midi sachant qu’elle en vend 200 de plus le matin que l’après midi. Combien avait-elle de gaufres au départ ?
Pour la résolution, le formateur peut proposer la séquence de schématisation suivante (en utilisant des objets déplaçables ou non):
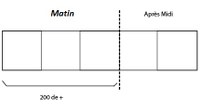
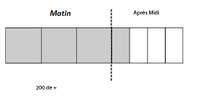
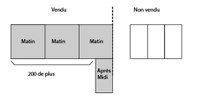
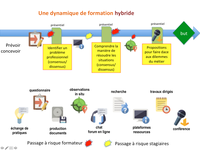
Temps1 RAMENER DES TRACES DU RéEL (DISTANCIEL)
Proposer à distance, deux semaines avant la session en présentiel un questionnaire (voir encadré ci-contre) aux enseignants pour faire un état des lieux de ce qu’ils font. Ce qu'ils savent bien faire et qui donne satisfaction, et ce qui leur pose problème, qu'ils voudraient faire mais qu'ils n'arrivent pas encore à bien faire.
Une semaine/quelques jours avant la formation voire le jour de la formation, le formateur collecte les réponses et les envoie à tous les participants, sans filtre ou traitement préalable, et annonce que le traitement des réponses constituera le premier temps de la formation en catégorisant les types de réponses. L'objectif étant de prendre conscience que même lorsqu'on pratique le même métier, nos préoccupations ne sont pas toujours les mêmes et ne s'expriment pas de la même façon.
Temps 2 catégoriser (presentiel)
- Retour sur les questionnaires (voir encadré ci-contre)
- Visionnage collectif de la vidéo de Séverine et de la vidéo d'Ingrid


- Analyse des vidéos avec les enseignants
Temps 3 discussion et Synthèse du temps de categorisation (presentiel)

Identifier avec les enseignants que des connaissances et des compromis opératoires sont nécessaires dans la mise en oeuvre de manipulations par les élèves ou par l'enseignant et que l'inhibition de la manipulation physique permet aux élèves de se représenter les problèmes mathématiques.
Identifier avec les enseignants les concepts de matérialité, d'objets déplaçables/non-déplaçables et d'objets modifiables/non modifiables
Temps 4 résoudre un problème en se plaçant dans la peau d'un élève (presentiel)
- Proposer la résolution de problème avec les outils/méthodes d'un élève de CM2/6ème (Le problème doit être résistant et donnera la possibilité d'un apport par la manipulation)
- Les enseignants se questionneront sur la nature de la manipulation, le moment où elle intervient, le choix de la schématisation, le tissage enter la réussite du problème, les stratégies mises en oeuvre, les connaissances utilisables/utiles/utilisées et les savoirs à institutionnaliser.
Temps 5 bilan
Faire le point sur ce que les enseignants retiennent de la formation, ce qu'ils sont prêts à expérimenter, seuls et/ou collectivement.
Références bibliographiques
- L'innovation pédagogique (2017) d'André Tricot dans la collection "mythes et réalités, aux éditions Retz
"Pourquoi faudrait-il alors aller à l’école ? Une réponse à cette question tient en quelques mots : parce que grandir ne suffit pas, parce que les connaissances apprises en interagissant avec notre environnement ne suffisent pas pour devenir des adultes, capables de comprendre et d’agir dans la société qui sera la nôtre dans quelques années. Les enfants des sociétés sans école apprennent énormément de connaissances, mais ils n’apprennent pas à lire, à écrire, à compter (ou, plus exactement, ils n’apprennent que ce qu’ils font quotidiennement, de sorte que s’ils comptent tous les jours, ils apprendront à compter avec des personnes de leur entourage)"
- Les premiers apprentissages scolaires à la loupe (2016), Claire Margolinas et Marceline Laparra, aux éditions DeBoeck
"Objet de l’univers matériel de l’élève, la gomme est utilisée pour recréer une surface vierge sur laquelle recommencer à travailler plutôt que pour faire disparaître une erreur. Dans une situation de manipulation, le fait d'ajouter ou d'enlever un objet tangible (un jeton existe toujours même lorsqu'on l'enlève) peut sembler correspondre au rôle joué par la gomme et le crayon. En réalité les situations sont très différentes puisque dans les situations sur fiche, "ajouter" revient à dessiner au crayon et "enlever" revient à gommer (dans ce cas l’objet n’existe plus). Ce sont là des actions relevant de la littératie chronotopique."
- Mettre au centre la résolution de problème (2014), de Pierre Eysseric dans les cahiers pédagogiques
"La manipulation semble s’imposer comme méthode naturelle d’apprentissage du nombre la plus compatible avec l’âge et le développement des enfants. Pourtant, peut-on envisager l’apprentissage du nombre, concept abstrait, construction de l’esprit humain, en restant dans le registre de la manipulation d’objets matériels ? Quelles formes de manipulations favorisent ou font obstacle à l’accès au concept de nombre ?"
- Représentation des problèmes et réussite en mathématiques, un apport de la psychologie cognitive à l'enseignement (1995) de Jean Julo aux presses universitaires de Rennes
"Les données actuelles de la psychologie cognitive nous permettent de mieux comprendre comment la représentation d'un problème mathématique se met en place. Ce livre s'adresse à ceux dont le métier est (ou sera) d'enseigner les mathématiques, ainsi qu'aux étudiants (psychologie, sciences de l'éducation) ; il vise à les aider à mieux comprendre ceux qui ont de la difficulté à construire des représentations performantes."