Les nombres décimaux
Objectifs de la formation
|
Concevoir des formations pour aider les enseignants à faire réussir tous les élèves
|
- Comprendre et utiliser la notion de nombre décimal
- Comprendre les principes et les usages des différentes écritures d'un nombre décimal
- Se familiariser avec les nombres décimaux au cycle 3
Format : Interdegré - CM1 et CM2 avec la pensée de la 6ème en tête, deux fois un jour et un temps d'inter-session entre les deux jours
Proposition de Déroulement
|
|
Enseignant |
Description |
Focales de Goigoux ? Principes de Reuter ? |
Intérêt/limite |
|---|---|---|---|
|
David |
|
|
|
|
Marie |
|
|
|
A partir des vidéos, le formateur peut faire remarquer:
Comprendre l'écriture, deux parties pour un seul nombre ? : " la finalité de l'apprentissage est de montrer que dans un nombre décimal il y a deux parties. Pour faire comprendre cela, David dans la vidéo 1 chapitre 1, s'appuie sur le schéma de Vergnaud "partie/partie//tout". Il insiste sur l'importance de la valeur de chaque chiffre dans le nombre '' Je ne veux pas la position, mais je veux la valeur'', il dit et il pose qu'il y a deux choses différentes. Il semble que c'est ce savoir-là que David veut construire; à 3'15'' il dit '' Je veux que vous vous rappeliez que dans un nombre décimal, il y a deux parties, la partie entière et la partie décimale''. Savoirs disciplinaires mobilisés par David: Il a en tête la classe de 6ème où les élèves apprennent qu'un nombre décimal est la somme de sa partie entière et sa partie décimale: 1,61=1+0,61 et la partie décimale est strictement inférieure à 1. On peut faire le parallèle avec la vidéo de Marie qui travaille dans l'autre sens".
Les principes de l'écriture décimale en base 10: "Dans la vidéo 2 à 1'15'', pour faire comprendre la décomposition canonique, David part du nombre 234,56 et fait verbaliser la valeur de chaque chiffre en s'appuyant sur le tableau des valeurs. On peut faire le parallèle avec la vidéo de Marie qui travaille dans l'autre sens. Elle fait écrire un nombre décimal à partir de sa décomposition en quantités, la question centrale semble être: "Comment fait-on pour trouver une écriture économique à partir de quantités?"
 Construction d'un savoir par un élève, cohérence de l’élève : illustration de la construction de savoir par un élève et de la manière dont l’enseignant et les pairs s’en emparent. David vidéo n°2 à 2’44, l'élève dit « j’ai remarqué que dixièmes c’est comme les dizaines » (remarque sur la symétrie inversée partie entière et partie décimale).Le formateur peut demander: "Qu’est-ce qu’on n’a pas remarqué et que les élèves remarquent dans l’écriture décimale ?" et faire remarquer "que l'élève donne un 'coup de pied' dans l’explication souvent donnée, les centièmes c’est deux chiffres après la virgule "
Construction d'un savoir par un élève, cohérence de l’élève : illustration de la construction de savoir par un élève et de la manière dont l’enseignant et les pairs s’en emparent. David vidéo n°2 à 2’44, l'élève dit « j’ai remarqué que dixièmes c’est comme les dizaines » (remarque sur la symétrie inversée partie entière et partie décimale).Le formateur peut demander: "Qu’est-ce qu’on n’a pas remarqué et que les élèves remarquent dans l’écriture décimale ?" et faire remarquer "que l'élève donne un 'coup de pied' dans l’explication souvent donnée, les centièmes c’est deux chiffres après la virgule "
Phase 5 : Apports théoriques et alternatives (temps 3)
- Enjeu de cohésion de pratiques d’équipe – cohésion de cycle: Vidéo Marie entretien chapitre 5 du début jusqu’à 11’08 et 11’40 jusqu’à 12’18
- A partir de l’observation des enseignants Marie et David et des pratiques du collectif d’enseignants sur cette question : quelles propositions ou autres pistes ? Le formateur sollicite la réflexivité des stagiaires.
- Apports théoriques et prescrit EDUSCOL(cycle 3) , EDUSCOL(cycle 4), registres sémiotiques (Eduscol), (Raymond Duval), Rationnels et nombres décimaux (Guy Brousseau)
-
Conférence de consensus du CNESCO
- Quel apprentissage de la notion de nombre ? par Henri Lehalle et Laetitia Desmet
- Quelle difficulté dans l'écriture des nombres ? par Marie-Pascale Noël
- Quels enjeux du calcul à l'école primaire ? par Eric Roditi et Jean-Paul Fisher
- Proposition d'outils: Le glisse-nombre et son utilisation (M@gistère ''enseigner le calcul mental au CM1 CM2'', cf.présentiel 1 puis vidéo 3 séances de calcul mental, à 1'45'', puis de nouveau à 8'40'', à 10' et 14'50''), la boîte à mystère, Groupe de travail de l'APMEP, Histoire des maths (Chercher avec la loupe "Simon Stevin" ou "nombre décimal" )
JOUR 1 C'est quoi le problème ? (En présentiel)
Temps 1 Le problème : Pourquoi de nouveaux nombres ?
La notion de nombre décimal est un nouveau savoir à enseigner qui bouscule des savoirs antérieurs, trois enjeux pour la formation:
- Enseigner l'écriture d'un nombre décimal: deux parties pour un seul nombre ?
- Enseigner des règles d'ordonnancement nouvelles
- Enseigner un nouveau lexique
Temps 2 Représenter les nombres décimaux


- Comprendre l'écriture: deux parties pour un seul nombre ? (Deux activités/tâches pour un même objet d'observation: l'écriture décimale)
- Les principes de l'écriture décimale en base 10 (deux démarches pédagogiques à analyser avec les focales de Goigoux)
Temps 3 Apports théoriques et alternatives
Questionner avec les stagiaires :
- La nature (concept) des nombres décimaux
- L'origine (histoire) des nombres décimaux
- L'écriture des nombres décimaux
- Les mots pour dire les décimaux
- La prise en compte des savoirs construits par les élèves ou leurs erreurs


|
|
Inter-session Développer sa pratique et son questionnement (distanciel)
Entre les deux jours de formation, le formateur peut proposer aux stagiaires de:
-
Mettre en œuvre en classe en fonction de ce qui a été vu, ou partir des propositions des collègues
-
Ordonner, comparer, calculer : apporter des éléments de sa pratique sur ces entrées
JOUR 2 Ordonner, comparer et calculer avec les nombres décimaux (En présentiel)
Temps 1 Retour sur les éléments apportés par les stagiaires
- Retour sur les essais dans la classe en inter-session
- Les apports sur "Ordonner, calculer et comparer avec les nombres décimaux"
Temps 2 Ordonner et comparer les nombres décimaux
- Visionnage collectif de la vidéo de Marie
- Analyse de la vidéo
Temps 3 Calculer avec les nombres décimaux
- Visionnage collectif chapitre 3 de la vidéo de Marianne
- Analyse de la vidéo
Temps 4 Discussion et synthèse
Le formateur pourra prendre quelques éléments de la conférence de consensus sur le nombre et les calculs en primaire, du CNESCO et tisser des liens avec les stagiaires sur l'ensemble du travail mené sur la formation sur la journée puis sur les deux jours.





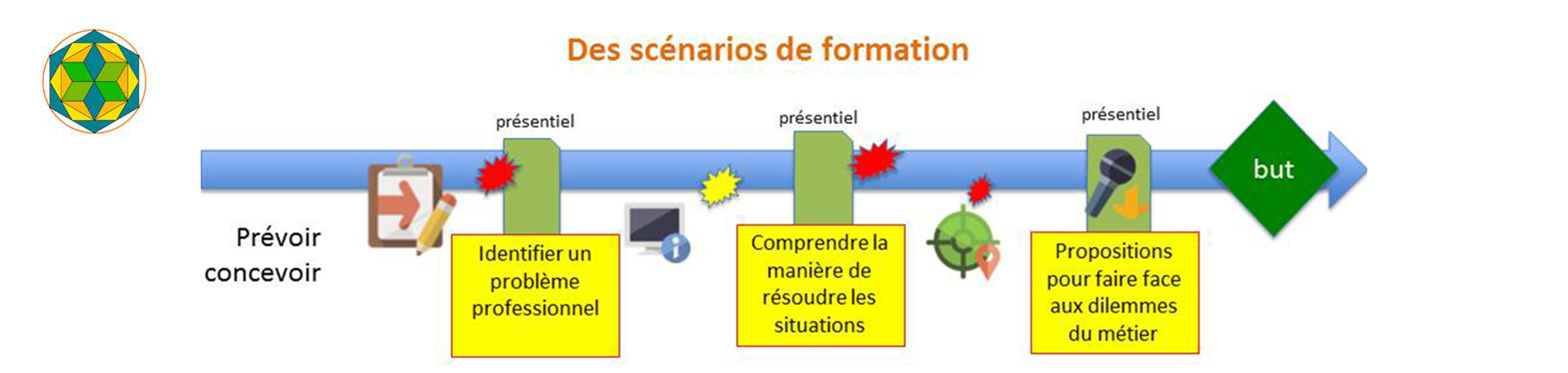
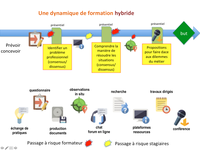
 Outillages conceptuels, méthodologiques et techniques
Outillages conceptuels, méthodologiques et techniques
 Après visionnage de la vidéo de
Après visionnage de la vidéo de  Discussion et synthèse (temps 4)
Discussion et synthèse (temps 4)