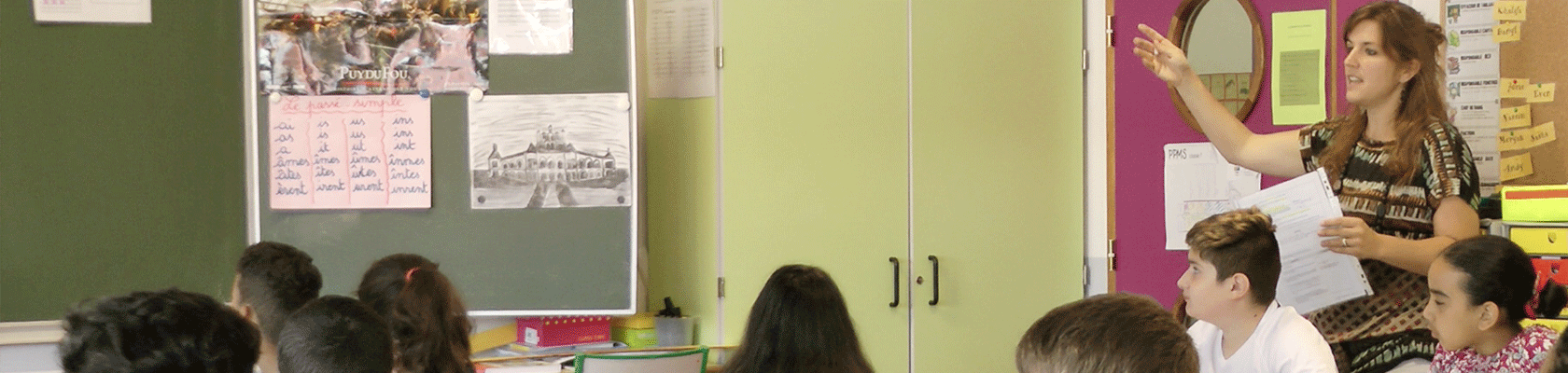Marianne - CM2 - Entraînement aux calculs posés.
Fin d'année scolaire, Marianne, enseignante en classe de CM2 engage les élèves dans le rituel du matin, une séance d'entraînement aux calculs posés (les quatre opérations). Cette séance se déroule en classe entière et a pour objectif l'automatisation des algorithmes. Chaque élève travaille individuellement sur une feuille d'exercices et doit faire vérifier son résultat par l'enseignante afin de valider un niveau de ceinture lui permettant de passer un niveau de difficulté supérieure :“ Y a plein de calculs et de ceintures, on doit essayer de bien faire pour aller le plus loin possible” rapporte une élève en début de séance. L'enseignante circule dans la classe, vérifie les résultats de chaque élève, questionne sur les procédures, fait corriger les erreurs et refaire les opérations erronées avant de valider les ceintures. Les élèves sont au travail, concentrés sur leur tâche; l’enseignante les invite à compter à voix haute et à utiliser les tables comme outils lorsque nécessaire. Dans l’entretien, Marianne explique qu'elle a accepté de travailler depuis quelques années, comme un grand nombre d'enseignants de l’école, à partir d'une méthode proposée par le M+ et éprouvée par quelques collègues. Elle fait part de son attachement au travail d'équipe, du questionnement professionnel qu’il génère pour elle. Par exemple concernant sa difficulté à enseigner les “grandeurs et mesures”, notion pour laquelle les élèves ont des résultats insatisfaisants, Marianne pense que le travail de l’équipe doit porter sa réflexion autour de l’enseignement de ces notions car “ce qui est abstrait ne marche pas”.
| player1 | |
| 1.Le fonctionnement des ceintures dans l'école, appliqué aux calculs | 00 : 00 |
| 2.Premier cas d'élève | 00 : 32 |
| 3.Deuxième cas d'élève | 02: 59 |
| 4.Troisième cas d'élève | 04 : 38 |
| 5.Un élève valide une ceinture | 05 : 29 |
| 6.Entretien Marianne - Un outil commun : une méthode proposée par le maître + | 07 :15 |
| 7.L'importance du travail d'équipe | 08 : 40 |
|
Description activité de l'enseignant |
Focales de Roland Goigoux --> Principes de fonctionnement collectif d'Yves Reuter --> |
Questions Questions | |
|---|---|---|---|
|
1.Le fonctionnement des ceintures dans l'école, appliqué aux calculs |
Début de séance de calcul posé (les quatre opérations), une élève interrogée par l'enseignante rappelle et explique à la classe, le fonctionnement des ceintures, inspirée du judo. La séance démarre, Marianne circule entre les tables et vérifie les résultats de chaque élève. |
Planification le rôle de l'évaluation Différenciation modalités tâches similaires ou différentes |
Motivation par l'émulation et la réussite (marquée par la ceinture) Rentrer dans la tâche par le rituel Rendre visible les progrès (pour l'élève) Individualiser, prendre le temps de passer de l'un à l'autre |
|
2. Premier cas d'élève |
L'enseignante passe du temps à une difficulté déjà rencontrée par un élève (soustraction avec retenue), l'interroge sur sa technique opératoire , lui rappelle les règles de fonctionnement de l'algorithme et l'invite à refaire ses opérations. L'élève seule refait ses soustractions. |
Planification: Tâche didactique Régulation -retour d'information (Feed-back immédiat) -traitement des erreurs Explicitation procédures ou stratégies |
Calcul posé, soustractions avec des nombres décimaux Position et valeur du chiffre dans le nombre La soustraction : entre sens et technique |
|
3. Deuxième cas d'élève |
L'enseignante interroge un élève pour comprendre pourquoi il a inversé les nombres des soustractions, alors qu'il ne fait pas cette erreur habituellement ; |
Planification: Tâche didactique Régulation - retour d'information (Feed-back immédiat) - traitement de l'erreur Explicitation procédures ou stratégies |
Calcul posé, soustractions avec des nombres décimaux Position et valeur du chiffre dans le nombre La soustraction : entre sens et technique |
|
4. Troisième cas d'élève |
Une élève fait une erreur dans les calculs posés liée aux tables de multiplications et non à la technique de la multiplication posée. L'enseignante lui conseille d'utiliser ses tables et de les utiliser autant de fois qu'il est encore nécessaire. |
Régulation étayage |
Calcul posé, multiplication Etayer les apprentissages pour rendre les élèves plus autonomes |
|
5. Un élève valide une ceinture |
Un élève valide une ceinture, un autre élève lui explique les « dangers », difficultés qu'il va rencontrer dans la prochaine ceinture à valider. |
Régulation: coopération et entraide Motivation enrôlement et maintien de l'engagement des élèves dans la tâche |
Calculs posés, qui requièrent de l'expertise (avec des grands nombres) Développer l'entraide et le tutorat pour la réflexivité chez les élèves. Motivation par l'émulation et la réussite (marquée par la ceinture) |
|
6. Entretien Marianne Un outil commun : une méthode proposée par le maître + |
Marianne a la conviction qu'utiliser une même méthode dans l'école, sur plusieurs années et dans les différents cycles, ça marche. |
Planification - tâche didactique - objectifs - démarche pédagogique |
Oser de nouveaux outils, une aide ou une difficulté supplémentaire |
|
7. L'importance du travail d'équipe |
Marianne dit qu'à dix-sept enseignants, c'est difficile de se mettre d'accord mais le travail en équipe c'est important pour se remettre en question et partager les pratiques de chacun. |
Solidarité de l'équipe |
Travailler seul sans partager/discuter ses pratiques vs travailler ensemble en acceptant d’être bousculé. |