La construction du nombre au cycle 1
Dans cette conférence, Rémi Brissiaud réaffirme l'importance d'enseigner le comptage-dénombrement pour permettre aux élèves de construire le concept de nombre. Il présente également un outil numérique qui permet cet enseignement : "Les Noums".
| player1 | |
| Pourquoi tant d’échecs dans la construction du nombre | 00:00:00 |
| Comment reconnaître, en début de CP, un élève qui a des difficultés à rentrer dans le nombre ? | 00:15:36 |
| L’itération de l’unité dans les programmes | 00:26:53 |
| Comptage-numérotage ou comptage-dénombrement ? | 00:28:44 |
| Une situation problème présentée à tort comme "la situation fondamentale de construction du nombre comme mémoire de la quantité" | 00:46:36 |
| L’usage de la file numérotée | 01:01:10 |
| Les Noums | 01:04:59 |
1- évolution des performances en calcul des élèves de CM2: l'analyse de Rémi Brissiaud
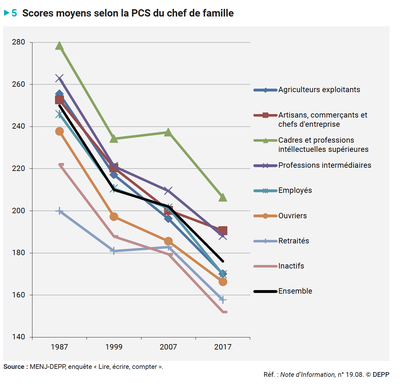
En 2017, la reprise d’une enquêteNote d'information de la DEPP N°19.08, Mars 2019 initiée en 1987, portant sur le calcul en fin de CM2, permet de comparer les performances des élèves à trente ans d’intervalle. Cette enquête donne des résultats à quatre temps de mesure : 1987, 1999, 2007 et 2017. Entre 1987 et 1999, les performances des élèves avaient fortement baissé. Cette tendance s’était atténuée entre 1999 et 2007. Dix ans plus tard, on assiste à une baisse des performances des élèves moins marquée cependant qu’entre 1987 et 1999. Cette baisse touche dans les mêmes proportions tous les élèves, quelque soit leur origine sociale.
Dans La psychologie de l'enfant, 1966, Jean Piaget propose une théorie du développement de l'intelligence chez l'enfant. Selon le biologiste, l'intelligence chez l'enfant est linéaire et cumulative. Elle est liée, stade après stade, à l'idée d'acquisition et de progrès, selon "le modèle de l'escalier". Tous ces stades se succèdent dans le même ordre pour tous les enfants. Rémi Brissiaud explique que pour Jean Piaget, l'enfant de maternelle n'est pas conservant (c'est-à-dire que si on déplace une collection d'objets dont il a perçu la quantité, celle-ci n'est plus perçue après le déplacement). Il le devient vers 7 ans, à "l'âge de raison". Il n'aurait donc pas le niveau de maturation nécessaire pour entrer dans le concept de nombre avant l'âge de 7 ans. Ces aspects de la théorie piagétienne irriguaient l'enseignement dans les années 70 et 80, période à laquelle les élèves de CM2 évalués en 1987 étaient scolarisés en maternelle. Ces élèves, au nom de la théorie piagétienne, ont donc bénéficié d'apprentissages pré-numériques lorsqu'ils étaient scolarisés en maternelle, mais pas d'apprentissages numériques, ceux-ci débutant réellement au mois de janvier de l'année de CP.
Les théories piagétiennes, notamment le modèle de l'escalier, sont remises en cause aujourd'hui. Du moins, les nouvelles théories psychologiques du développement de l'enfant indiquent que ce modèle n'est plus le seul possible. Il existerait déjà chez les bébés des capacités cognitives complexes, c'est-à-dire des connaissances physiques, mathématiques, logiques et psychologiques ignorées par Jean Piaget et non réductibles à un fonctionnement strictement sensori-moteur.
Pourtant, Rémi Brissiaud relève ici un paradoxe: ce sont ces élèves scolarisés en maternelle au début des années 80 qui surperforment les élèves scolarisés en maternelle au début des années 2010. Il souligne l'intérêt des travaux de Jean Piaget du point de vue de la construction du nombre. Jean Piaget s'est intéressé aux propriétés des actions de l'enfant. Ces propriétés renvoient à la situation suivante : j'ai une certaine quantité; si j'ajoute des quantités, puis que je les retire, c'est toujours la même quantité. Jean Piaget définissait le nombre comme la construction d'un variant opératoire, c'est-à-dire que pour résoudre une opération, il est possible d'avoir recours à plusieurs modalités de résolution.
L'effondrement des performances des élèves en calcul, selon Rémi Brissiaud, est corrélé à l'introduction de l'enseignement du comptage-numérotage en 1986, enseignement qu'il qualifie comme étant "à rebours des recommandations de nos prédécesseurs dans le métier".
2- comment reconnaître, en début de CP, un élève qui va avoir des difficultés à rentrer dans le nombre ?
Les élèves, se retrouvant en difficulté en début de CP dans la construction du nombre, sont ceux qui n'ont pas construit la propriété de l'itération de l'unité. Ce sont ces élèves qui, en entretien individuel aux vacances de la Toussaint de l'année de CP, lorsqu'on leur pose la question : "Donne-moi 4 jetons", procèdent au comptage numérotage (un, deux, trois, quatre, ça fait quatre jetons). Puis à la question: "Maintenant, donne-moi 5 jetons", ils recommencent le comptage-numérotage (un, deux, trois, quatre, cinq, ça fait cinq jetons) plutôt que de donner simplement un cinquième jeton. Ces élèves savent construire une collection de 4 ou 5 objets par comptage-numérotage, mais ils ne savent pas mettre en corrélation ces 2 quantités (le fait que 5, c'est 4 et encore 1). Ou du moins, ils ne savent pas réinvestir cette propriété de l'itération de l'unité (5, c'est 4 et encore 1) en situation de résolution de problème.
La question "Combien ça fait 4 + 1 ?" peut donner l'illusion que l'élève, s'il répond correctement, maîtrise la propriété de l'itération de l'unité. Dans cette situation, il faut être vigilant à la procédure que mobilise l'élève pour y répondre. En effet, il peut avoir recours à la frise numérique et regarder le chiffre immédiatement après le chiffre 4. Dans ce cas, sa réponse, bien que correcte, ne signifie pas qu'il maîtrise la propriété de l'itération de l'unité, qui est la propriété conceptuelle fondamentale du nombre. L'élève a construit ici un savoir qui peut être qualifié de "verbal", mais qui ne coïncide pas avec un savoir "opérationnel", mobilisable en situation de résolution de problèmes. Or les propriétés conceptuelles sont celles qui structurent un domaine de connaissances, qui relient les connaissances élémentaires entre elles. L'enfant qui ne maîtrise pas ces propriétés conceptuelles est typiquement l'enfant qui sera en difficulté en mathématiques. Les progressions de mathématiques devraient, selon Rémi Brissiaud, être construites à partir des propriétés conceptuelles.
3- L'itÉRATION DE L'UNITÉ DANS LES PROGRAMMES
À l'école maternelle
Dans les programmes de l'école maternelle de 2015B.O. spécial n°2 du 26 mars 2015 , auxquels Rémi Brissiaud a contribué, l'itération de l'unité occupe une place centrale. Elle est abordée dans l'axe 4 des programmes, "Construire les premiers outils pour structurer sa pensée", mais pourrait être enrichie (l'itération de l'unité, c'est aussi dire que 4, c'est 3 et encore 1, que 5 c'est 4 et encore 1, etc...)
|
Page 16
|
Page 17
|
Au cycle 2
En mathématiques, dans les programmes de cycle 2 en vigueur depuis la rentrée 2018 B.O. du 26 juillet 2018, la propriété de l'itération de l'unité est abordée de la manière suivante (page 68):

Mais, selon Rémi Brissiaud, l'opérationnalisation de la phrase [comprendre que le successeur d'un nombre entier c'est "ce nombre plus un"] est indispensable pour accompagner les enseignants à valider la compréhension du concept de l'itération de l'unité par les élèves.
4- comptage-numérotage ou comptage-dénombrement ?
Le comptage-numérotage et le comptage-dénombrement ne font pas le même usage des mots-nombres. Dans le comptage-numérotage, les mots-nombres sont des numéros et privilégient l'aspect ordinal du nombre alors que dans le comptage-dénombrement, ils désignent des quantités, l'aspect cardinal du nombre. Ce qui fonde le nombre, selon Rémi Brissiaud, c'est son aspect cardinal.
Le comptage-numérotage
Les programmes de l'école maternelle de 2015 spécifient également que "les activités de dénombrement doivent éviter le comptage-numérotage", page 17. Mais à quoi correspond le comptage-numérotage ?
Selon Rémi Brissiaud, enseigner le comptage-numérotage, c'est théâtraliser la correspondance terme à terme, en faisant correspondre un mot-nombre avec une unité. Pour l'élève, le nombre réfère alors à l'objet pointé, comme lorsqu'un adulte prononce un mot nouveau en pointant du doigt un objet (ex: "regarde le chien"). Des psychologues spécialistes de l'acquisition du langage, comme Elen Markman (1990), ont étudié les hypothèses que font les enfants lorsque les adultes pointent un objet et prononcent un mot nouveau en même temps. En aucun cas l'enfant ne va faire l'hypothèse que le mot nouveau qui est prononcé renvoie à quelque chose sans rapport direct à l'entité qui est pointée. Dans l'exemple que donne Rémi Brissiaud ici, le mot-nombre "cinq" est prononcé en pointant un et un seul lapin, le cinquième lapin, alors que l'enfant devrait comprendre que ce mot-nombre renvoie à une quantité (tous les lapins pointés avant et avec ce cinquième lapin). Il est alors probable que dans ce contexte de comptage-numérotage, l'enfant construise une signification du mot-nombre "cinq" qui correspond à sa valeur ordinale, au numéro 5.
Selon Rémi Brissiaud, la stratégie de comptage-numérotage est une stratégie de bas niveau. Son enseignement enferme l'élève en difficulté. Il accède difficilement au concept de nombre. Il a appris que le dernier mot prononcé désigne une quantité, mais il ne maitrise pas la propriété de l'itération de l'unité, nécessaire pour entrer dans le nombre et le calcul.
Le comptage-dénombrement
La recommandation d'enseigner le comptage-dénombrement n'est pas nouvelle. On la trouve déjà en 1962, dans les écrits de René Brandicourt, directeur d'école d'application et pédagogue, co-auteur d'un ouvrage consacré aux premiers apprentissages numériques avec Jeanne Bandet, Inspectrice Générale des écoles maternelles et Gaston Mialaret, l'un des créateurs des Sciences de l'Éducation en France. René Brandicourt imagine des assiettes alignées devant lui. Pour les dénombrer, il va les prendre l'une après l'autre en formant une pile. Il écrit dans cet ouvrage : « à ce sujet [...], nous signalons le danger qu'il y a, dans le comptage, à énoncer les nombres en prenant les objets un à un". Il continue "c'est en posant la 2e assiette sur la 1re que je dis 2, non en la prenant en mains (la 2e n'est pas 2, elle est 1) ; ibid. pour la 3e, la 4e... C'est en examinant la pile successivement constituée que j'énonce 2, 3 , 4... 6. »
Dans ces conférences, et dans le prolongement des travaux de René Brandicourt, Rémi Brissiaud recommande de compter-dénombrer en disant "1 et encore 1, 2...", en regardant la pile des 2 assiettes, "... et encore 1, 3...", en regardant la pile des trois assiettes, "... et encore 1, 4". Il recommande également d'enseigner le comptage-dénombrement à l'école, surtout que l'itération de l'unité sur les cinq premiers nombres se construit dans l'ordre. Cela signifie que l'enfant construit le nombre 5 (5, c'est 4 et encore 1) que s'il a construit le nombre 4 (4, c'est 3 et encore 1), etc... En découle la progression suivante à l'école maternelle:
- En petite section, privilégier la compréhension des 3 premiers nombres. Il s'agit de travailler d'abord les nombres 1 et 2, puis d'introduire le nombre 3 (3, c'est 2 et encore 1, mais aussi grâce au subitizing comme 3, c'est 1, 1 et encore 1).
- En moyenne section, revoir les 3 premiers nombres et introduire le nombre 4 (4, c'est 3 et encore 1), le nombre 5 (5 c'est 4 et encore 1), puis travailler ces nombres avec d'autres types de décomposition/recomposition (4, c'est 2 et encore 2).
- En grande section, revoir les 5 premiers nombres et privilégier les décompositionsRémi Brissiaud, Le nombre dans les nouveaux programmes de maternelle, deuxième partie, café pédagogique, octobre 2015, en premier, celles du type 5 + n et, en second, les décompositions des nombres pairs en doubles et celles des nombres impairs en doubles + 1. L'accès aux décompositions suivantes, par exemple, doit être considéré comme prioritaire : 6 = 5 + 1 (itération de l'unité), 6 = 3 + 3 (double), 7 = 6 + 1 (itération de l'unité), 7 = 5 + 2 (repère 5), 7 = 3 + 3 + 1 (double +1), 8 = 7 + 1 (itération de l'unité), etc...
5- Une situation problème présentée à tort comme "la situation fondamentale de construction du nombre comme mémoire de la quantité"
 Rémi Brissiaud, dans ce chapitre, décrit une situation-problème considérée comme "la situation fondamentale de construction du nombre comme mémoire de la quantité". Dans cette situation, les élèves sont face à une quantité de pots et sont invités à répondre à une commande : aller chercher au fond de la classe où sont rangés les pinceaux, la même quantité de pinceaux que de pots, en un seul déplacement.
Rémi Brissiaud, dans ce chapitre, décrit une situation-problème considérée comme "la situation fondamentale de construction du nombre comme mémoire de la quantité". Dans cette situation, les élèves sont face à une quantité de pots et sont invités à répondre à une commande : aller chercher au fond de la classe où sont rangés les pinceaux, la même quantité de pinceaux que de pots, en un seul déplacement.
Cette situation est analysée par Rémi Brissiaud comme une situation d'apprentissage du comptage-numérotage. Elle ne permet pas par conséquent de construire le nombre. Pour étayer son propos, il montre que le recours aux lettres de l'alphabet pour résoudre ce problème est aussi efficace que de recourir à la comptine numérique. En effet, il suffit de réciter A, B, C, D, E, F, G en pointant chacun des pots, de garder en mémoire la dernière lettre prononcée (G) et de réitérer cette procédure au fond de la classe pour les pinceaux. Par conséquent, le recours au comptage-numérotage donne l'illusion que l'élève construit le nombre, or il n'en est rien. La récitation de la comptine numérique lui permet juste de garder en mémoire le dernier nombre prononcé comme indicateur de la quantité. Cette situation ne permet pas à l'élève de construire l'itération de l'unité, de comprendre que 8, c'est 7 et encore 1, ou que H, c'est G et encore A. Quelle que soit la quantité de pots proposée, l'élève en difficulté recommencera son comptage-numérotage depuis le début pour résoudre le problème. Il ne construira aucune décomposition-recomposition des nombres. L'élève performant quant à lui, a toutes les décompositions du nombre 8 par exemple activées dans son cerveau (8 = 7 + 1, 8= 4 + 4, 8 = 10 - 2, etc...).
Rémi Brissiaud insiste ensuite sur la différence entre nombre et quantité. Ces deux notions, bien que liées, renvoient à des concepts différents. La notion de quantité nait de l'usage de la correspondance terme à terme alors que la notion de nombre nait de la comparaisons de quantités différentes, de l'accès à leurs différences, et plus tard, de l'accès à leurs rapports.
6- L'usage de la file numérotée
Selon Rémi Brissiaud, l'usage de la file numérotée enferme les élèves les plus fragiles dans le comptage-numérotage. L'alternative serait un affichage (ci-contre) qui théâtralise l'itération de l'unité. Les comparaisons internationales des performances des élèves en calcul entre la Chine de Taïwan et les États-Unis Recherche de Geary, Fan & Box-Thomas, 1992 montrent des écarts de performance importants. Les élèves chinois sont beaucoup plus performants que les élèves américains. Ceci s'explique en partie par l'enseignement du nombre aux États-Unis et au recours quasi systématique au comptage-numérotage en lien avec la file numérique.
7- LEs noums
Rémi Brissiaud terminer sa conférence en présentant un outil numérique, l'application "les Noums", qui permet de construire les bases de calcul et de résolution de problèmes au CP par la représentation mentale des quantités et une première modélisation. Agir sur le représentations permet à l'élève d'anticiper le résultat d'actions qui seraient menées dans la réalité.
Cet outil, qui prend la forme d'un jeu éducatif, peut être utilisé également dès la Grande Section. Il peut être utilisé soit sur des tablettes, soit via un tableau blanc interactif.
Les principes de fonctionnement des Noums
Deux modalités de travail : le "bac à sable" ou le quiz.
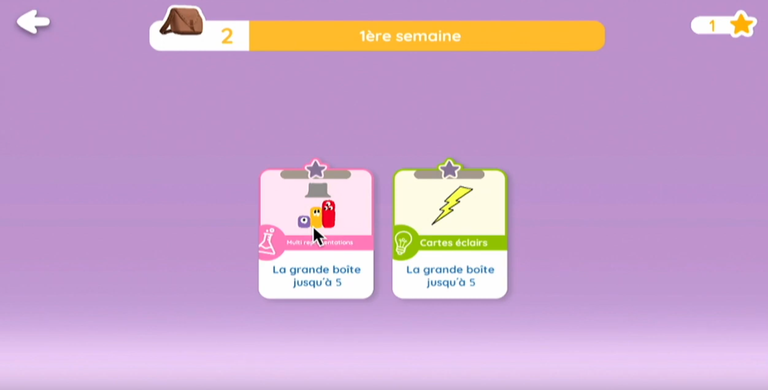
Dans ce jeu, le projet de l'année est de battre le monstre Osgard. Pour cela, il faut résoudre des calculs et des problèmes. A chaque séance, l'élève entre d'abord le code qu'il y a dans son fichier. Il a alors accès à deux propositions :
- un laboratoire pour découvrir un univers, tester des choses,
- un quiz, accompagné de feed-backs.
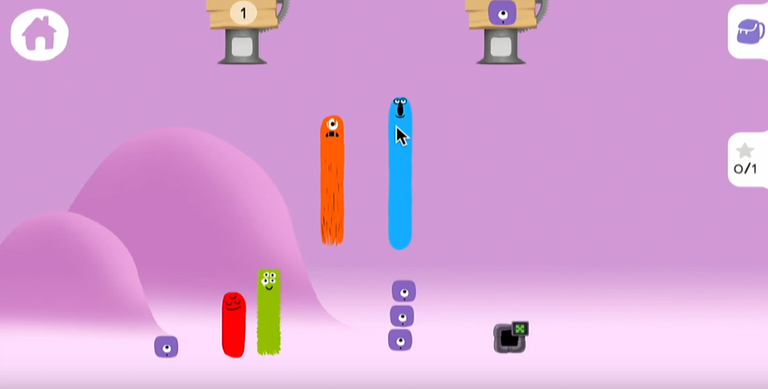
Des Noums inspirés des réglettes Cuisenaire
Dans le laboratoire, l'élève peut explorer les nombres. Chaque nombre a une taille et une couleur spécifique, en respectant les proportions (le Noum 2 est grand comme le Noum 1 et encore le Noum 1 par exemple), comme pour les réglettes Cuisenaire. Le fait de faire correspondre un Noum à une grandeur, sans monter à combien d'unités correspond cette grandeur (par exemple le Noum 3 est trois fois plus grand que le Noum 1, mais on ne voit pas les 3 unités qui le constituent) permet de construire les relations entre les quantités et évite le comptage numérotage (qui serait encouragé par l'utilisation physique de cubes par exemple).

Un outil pour travailler la représentation mental des nombres : le scanner des Noums
L'utilisation du scanner permet de travailler avec les élèves la représentation mentale des nombres, par exemple que le Noum 3 est composé de 3 unités. Rémi Brissiaud précise que le scanner fonctionne comme une métaphore de ce qu'il se passe dans le cerveau de l'enfant : il y a ce qu'il voit (le(s) Noum(s) ou l'assemblage de Noums) et il y a ce qu'il doit se représenter mentalement (le nombre d'unités que chaque Noum a dans le corps). L'anticipation est présente dans chacune des séances (par exemple, que va-t-il se passer si le Noum 2 mange le Noum 3 ?).

Un système d'aide à la mémorisation
Le nombre d'yeux que possèdent les grands Noums (de 6 à 9) en facilitent la mémorisation (un oeil pour le Noum 6 car 6, c'est 5 + 1, deux yeux pour le Noum 7 car 7, c'est 5 + 2, etc...). Ce système des yeux aide aussi à créer le repère 5.
Des situations d'anticipation
Le laboratoire permet d'autres situations d'anticipation avec le recours à la boite de 10 cases et des questions et manipulations de type : "si je mets le Noum 6 dans la boite, combien d'unités vais-je obtenir ?"
Bibliographie support au propos de R. Brissiaud
Brissiaud R. (2012). Dyscalculiques ou "mal débutés"? Les réponses de la comparaison 87-99-2007 (DEPP). ANAE. Approche neuropsychologique des apprentissages chez l'enfant, n°120-121, pp. 503-508.
Brissiaud R. (2013) Apprendre à calculer à l'école - Les pièges à éviter en contexte francophone. Paris. Retz.
Brissiaud R. (octobre 2014) Pourquoi l'école a-t-elle enseigné le comptage-numérotage pendant près de 30 années? Une ressource à restaurer: un usage commun des mots grandeur, quantité, nombre, numéro, cardinal, ordinal, etc. Texte mis en ligne par la Commission Française pour l'Enseignement des Mathématiques (CFEM).
Chabanon L. & Pastor J-M (2019). L'évolution des performances en calcul des élèves de CM2 à trente ans d'intervalles (1987-2017). Note 19.08 de la DEPP; mars 2019.
Rochet T. (2008). Lire, écrire, compter: les performances des élèves de CM2 à vingt ans d'intervalle 1987-2007. Note 08.38 de la DEPP; décembre 2008.
Revenir à l'ensemble des conférences sur les mathématiques (2018-2020) en cliquant sur cette icône







