DES ALGORITHMES ÉVOLUTIFS POUR ENSEIGNER LES OPÉRATIONS
| player1 | |
| Des algorithmes évolutifs pour enseigner les opérations arithmétiques | 00:00:00 |
| La genèse de l’addition | 00:01:22 |
| Les procédures de soustraction | 00:06:22 |
| Les procédures de multiplication | 00:11:46 |
Des algorithmes évolutifs pour enseigner les opérations arithmétiques
Comment mettre en place une construction progressive des opérations notamment pour les élèves en difficulté? Comment apprendre les mathématiques et pas seulement faire des mathématiques? Si on souhaite que l'élève s'engage et soit confiant, il est conseillé qu'il refasse à peu près la même chose chaque jour.
La genèse de l'addition
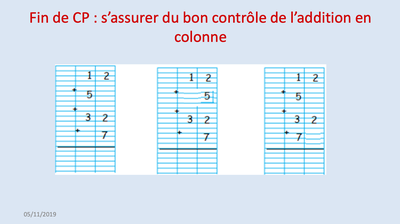
Une vidéo est présentée: dans une classe de CP, tous les jours, deux élèves doivent ramener le matériel nécessaire à la construction du nombre proposé par l'enseignante. Ensuite, elle mélange le matériel et demande d'ajouter ces deux nombres. Tous les élèves doivent prévoir par écrit ce qu'ils vont trouver. Cette micro-séquence d'apprentissage est la "colonne vertébrale" de la construction du concept d'addition dans cette classe.
Pour J. Briand, il est nécessaire d'accepter les différentes manières de faire des élèves pour arriver à la solution même celles qui ne seraient pas académiquement admises. Il appelle cela les algorithmes évolutifs, c'est-à-dire les étapes par lesquelles l'élève passe pour, à terme, arriver à poser une addition avec retenue.
L'addition ne devient révélateur de l'acquisition de la numération qu'à partir du moment où l'enseignant propose une addition de nombres à deux chiffres et à un chiffre. En effet, cela permet d'observer si l'élève organise ces chiffres correctement.
Les procédures de soustraction
À partir de la soustraction 125 - 97, plusieurs techniques sont présentées. L'idée est de voir en chacune d'elle les avantages et les inconvénients.
La technique par "démolition" ou à la canadienne :
Elle repose sur la démolition des dizaines pour alimenter les unités car elles sont en nombre insuffisant. L'avantage est qu'elle repose sur la compréhension de notre système d'écriture. Par contre, elle repose sur une manipulation donc le risque est que la soustraction ne soit qu'une démonstration de la manipulation et non une prévision.
La technique par "compensation ou translation" prend appui sur la droite graduée:

On peut trouver le résultat de 125-97 en faisant 128-100 sur une droite numérique. Pour que cette astuce devienne une méthode accessible à l'ensemble des élèves, l'enseignant doit réfléchir à quels outils mettre en place en classe.
Dans la méthode "à la russe", on cherche un nombre rond.
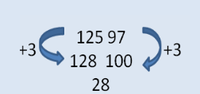
Cependant, il faut que l'élève ait des connaissances sur le glissement d'une bande sur la droite numérique, donc il est nécessaire qu'un travail soit fait sur les mesures de longueur en amont.
Dans la méthode usuelle en France, on ajoute systématiquement une dizaine lorsque le nombre d'unités est insuffisant. Cela revient alors à passer de 125-97 à 135-107 sur la droite graduée. Cette technique est moins astucieuse que la méthode à la russe mais elle est utilisable quels que soient les nombres choisis et s'appuie sur la technique usuelle de la soustraction en France. Par contre, elle nécessite de prendre le temps de travailler la propriété de conservation des écarts, sur laquelle elle repose.
Les procédures de multiplication
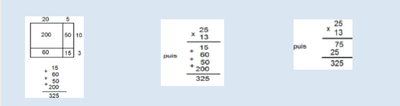
Un algorithme évolutif de la multiplication pourrait être dans un premier temps des calculs intermédiaires à l'aide d'un quadrillage, puis l'addition des calculs intermédiaires de la multiplication posée pour en arriver enfin à la méthode usuelle. Cette approche a été longuement étudiée en France depuis les années 80.
Revenir au dossier "Manipulation: questions d'enseignement et de formation" en cliquant sur cette icône





