Les usages de la langue en mathématiques : complexité, difficultés et leviers
| player1 | |
| Le Langage est constitutif de la Pensée | 00:00 |
| Quelle est la place de la langue dans le triptyque "Manipuler, verbaliser, abstraire" ? | 06:33 |
| Pratiques langagières des mathématiciennes et mathématiciens de métier | 09:05 |
| Usages de la langue dans la classe de mathématiques | 10:07 |
| En classe la complexité se traduit souvent en difficultés | 19:18 |
| Du côté des sciences du langage et de la didactique du français | 27:32 |
| La langue comme objet d'apprentissage en mathématiques | 31:54 |
| Des pistes en classe pour matérialiser la langue |
35:59 |
Le langage est constitutif de la pensée
Langage : « Capacité générale des êtres humains à s’exprimer et à communiquer à l’aide de signes », Définition du CNRTL.
Le langage n'est pas forcément la langue. Dans le socle commun de connaissances, de compétences et de culture (2016) on trouve 273 occurrences du terme langage. Il est souvent associé à des qualificatifs : le langage corporel, le langage cartographique, le langage verbal, etc.
« Il n’y a pas d’extériorité entre pensée et parole ou entre l’acte de penser, d’avoir des idées et l’acte de parler, de faire des phrases. L’idée ne préexiste pas au langage, elle se forme en lui et par lui. Le langage est le lieu d’exercice de la pensée : la pensée raisonne dans le langage pour se trouver et se dire » (Carol, 2015).Carol R.(2015). La didactique de l'enseignement bilingue : enseignement disciplinaire et langage. Recherches en didactique des langues et des cultures. http://journals.openedition.org/rdlc/973.
Dire que le langage est constitutif de la pensée implique qu'il n'y a pas de pensée sans langage et réciproquement il n'y a pas de langage sans pensée. Le langage est un outil de construction, de négociation et de transformation des représentations sociales et individuelles. Il est au coeur des processus d'enseignement et d'apprentissage.
La langue de son côté est un réservoir commun relativement stable. Chaque groupe social développe des pratiques langagières qui lui sont propres. Un groupe social d'enseignants et d'élèves qui travaille une discipline scolaire a des façons spécifiques d'utiliser la langue. On parle alors de pratiques langagières disciplinairesHache C.(2019). Questions langagières dans l'enseignement et l'apprentissage des mathématiques. Université Paris Diderot, 2019. https://hal.science/tel-02420979 .
« L'activité langagière est aussi une activité contextualisée qui s’organise dans des genres de discours spécifiques, en référence à Bakthine (1984), qui énonce que : « Si les genres n’existaient pas, il faudrait les inventer ». Sa définition du genre est celle d'une forme relativement stable qui permet d'organiser les énoncés selon les normes données par la culture.» (Rebière & Jaubert, 2021).Jaubert M. et Rebière M.(2021). Langages et construction de savoirs dans les disciplines scolaires : questionner des évidences. Conférence chapitrée sur le site du centre Alain-Savary. Lien vers l'article.
Quelle est la place de la langue dans le triptyque "Manipuler, Verbaliser, Abstraire" ?
Depuis le rapport Villani-TorossianTorossian C. et Villani C. (2018). 21 mesures pour l'enseignement des mathématiques.https://www.education.gouv.fr/21-mesures-pour-l-enseignement-des-mathematiques-3242 , la question des apprentissages en mathématiques fondés sur la manipulation, la verbalisation et l’abstraction est devenue centrale dans l’enseignement des mathématiques et les plans de formation. L'activité langagière de l'enseignant est présente sur tous les temps de ce triptyque.
Le rapport préconise des étapes d’apprentissage bien identifiées : l’étape concrète, l’étape imagée et l’étape abstraite. Si cette démarche est un cadre structurant pour l’enseignement, elles ne peut être exhaustive quant aux pratiques langagières qui l'accompagne.
«Le rapport Villani-Torossian pour l’enseignement des mathématiques [...] formule des recommandations en lien avec la démarche utilisée à Singapour pour mettre en œuvre un apprentissage des mathématiques fondé sur la manipulation et l’expérimentation, la représentation puis l’abstraction en incitant à une verbalisation par le professeur et par les élèves tout au long des apprentissages »(site Eduscol, consulté en mars 2025).
On trouve des convergences et des différences avec d'autres triptyques issus de la recherche.
Par exemple, le triptyque "Action, formulation, validation" est au coeur des travaux de Guy Brousseau. Bien qu'il soit ressemblant dans sa formulation, ici c'est le milieu d'apprentissage qui joue le rôle de médiation, l'enseignant étant plus à distance (le milieu est dit "antagoniste" dans la Théorie des Situations Didactiques de G.Brousseau, ndlr). Ainsi l'élève est conduit à agir, formuler ou valider les hypothèses qu'il a faites dans une situation (dite situation "a-didactique" dans la TSD, ndlr). Le tryptique est conclu par un moment où l'enseignant dit le savoir (dit moment "d'institutionnalisation" dans la TSD, ndlr).
«La formulation d’une connaissance correspondrait à une capacité du sujet à la reprendre (la reconnaître, l’identifier, la décomposer et la reconstruire dans un système linguistique). Le milieu qui doit rendre nécessaire l’usage par le sujet d’une formulation doit donc comporter (effectivement ou fictivement) un autre sujet à qui le premier devra adresser une information.La formulation des connaissances met en œuvre des répertoires linguistiques divers (syntaxe et vocabulaire). L’acquisition de ces répertoires accompagne celle des connaissances qu’ils expriment, mais les processus sont distincts.»(Brousseau, 1997).Brousseau, G.(1997). Cours donné lors de l’attribution à Guy Brousseau du titre de Docteur Honoris Causa de l’Université de Montréal. p.9.http://www.cfem.asso.fr/actualites/archives/Brousseau.pdf
Jean-Paul Bernié développe un autre triptyque indissociable "Agir-parler-penser". Ce triptyque met l'accent sur les dimensions langagières spécifiques de chaque discipline. Dans cette approche, l'enseignant à un rôle déterminant pour rendre lisibles ces éléments langagiers.
« Notre perspective didactique, inspirée des travaux de Léontiev et Vygotski, est fondée sur la nécessité pour l'élève d'intérioriser des savoirs et outils élaborés hors de lui, dans l'histoire, et déposés dans la culture. [...] L'un des problèmes posés à l'élève par l'entrée dans la culture écrite est qu'il tend à ne pas distinguer ce qui est dit de ce qui est signifié, autrement dit, à rester à une interprétation des énoncés qui lui sont proposés, conditionné par des pratiques communicatives immédiates[...] L'institution de l'enfant comme élève dans une discipline suppose qu'il distingue les manières d'agir-parler-penser de chaque discipline d'enseignement par rapport aux autres »(Bernié, 2002).Bernié J.P.(2002). L'approche des pratiques langagières scolaires à travers la notion de « communauté discursive » : un apport à la didactique comparée ?. In: Revue française de pédagogie, volume 141. Vers une didactique comparée. pp. 77-88. https://www.persee.fr/doc/rfp_0556-7807_2002_num_141_1_2917.
Complexité des pratiques langagières des mathématiciennes et mathématiciens de métier
Les pratiques langagières des mathématiciennes et mathématiciens de métier sont caractérisées par des formulations :
- qui contiennent de nombreux implicites, c'est à dire des présupposés nombreux ;
- dont l'usage est complexe et spécifique, comme la densité des concepts ;
- qui contiennent des variables mathématiques et la présence de quantificateurs comme par exemple : "Quelque soit ...", "Il existe...".Cori R.(2017). Ces fichues variables. Images des mathématiques. Les maths en mots et en images.https://imagesdev.math.cnrs.fr/billets/ces-fichues-variables/.
Le fait que ces pratiques soient largement inconscientes pour les acteurs complexifie la compréhension des formulations.
Complexité des usages de la langue dans la classe de mathématiques
Le mot " multiple" En arithmétique
 L'exemple ci-contre est issu des travaux de thèse de Zoé MesnilBarrier T.,Durand-Guerrier V. et Mesnil Z.(2019). L’analyse logique comme outil pour les études didactiques en mathématiques », Éducation et didactique, 13-1, 61-81.https://hal.science/hal-02070074/document..
L'exemple ci-contre est issu des travaux de thèse de Zoé MesnilBarrier T.,Durand-Guerrier V. et Mesnil Z.(2019). L’analyse logique comme outil pour les études didactiques en mathématiques », Éducation et didactique, 13-1, 61-81.https://hal.science/hal-02070074/document..
Ces deux phrases sont compréhensibles et vraies :
- dans la première, on dit que les nombres qui sont à la fois multiples de trois et de quatre sont des multiples de douze, ce qui signifie que 12 est le plus petit multiple commun de 3 et 4 ;
- dans la deuxième on dit que les multiples de six sont des multiples de trois et les multiples de neuf sont des multiples de trois, ce qui signifie que 3 est le plus grand diviseur commun de 6 et 9.
La même structure grammaticale de la phrase peut être interprétée de deux manières différentes en fonction des usages que l'on en fait. Comprendre les deux sens possibles de ces phrases est la marque d'une culture mathématique. Quand on lit des phrases avec un sens mathématique cohérent, on fait des mathématiques.
Le mot "rectangle" en géométrie
 Cet exemple est issu d'une expérience que le chercheur a vécue lors des rencontres MathsMonde organisées par l'IREMS de Paris en 2024. Lors de ces rencontres, il s'agit de décortiquer un thème selon le point de vue d'enseignants issus de pays différents.
Cet exemple est issu d'une expérience que le chercheur a vécue lors des rencontres MathsMonde organisées par l'IREMS de Paris en 2024. Lors de ces rencontres, il s'agit de décortiquer un thème selon le point de vue d'enseignants issus de pays différents.
Une enseignante exposait comment, en Angleterre, on résolvait le problème qui consiste à se demander si une règle de 35 cm est assez grande pour mesurer la diagonale d'une feuille de format A4. Cette enseignante a d'abord fait résoudre le problème par une collègue française. Ci-contre on peut voir la production langagière à l'écrit de l'enseignante qui donne à voir des spécificités et une difficulté de l'usage de la langue française en mathématique.
On observe que le mot rectangle apparait trois fois en trois lignes.
La nature grammaticale de ce mot peut être un nom (un rectangle) ou un adjectif (Le triangle est rectangle) :
- le nom rectangle renvoie à un type de quadrilatère particulier, c'est-à-dire un quadrilatère qui a quatre angles mesurant 90° ;
- l'adjectif rectangle renvoie à une propriété d'un triangle, c'est-à-dire l'un des angles du triangle mesure 90°.
Pour un élève, cette double interprétation peut être source de malentendu : "Comment un triangle peut être rectangle puisqu'un rectangle a quatre angles ? "
Logique des énoncés en géométrie
Les trois expressions ci-contre se ressemblent mais ont un sens différent. La différence entre les deux premières n'est pas claire.
En effet :
- Formuler " Si ABCD est un carré alors c'est un rectangle", c'est décrire une propriété générale des quadrilatères. Il manque une quantification qui se formule ainsi : " Quels que soient les points A, B, C et D, si ABCD est un carré, alors c'est un rectangle ". Les points A, B, C et D sont "muets", on pourrait exprimer la même propriété en substituant les points A, B, C, D par E, F, G, H ;
- Formuler " ABCD est un carré donc c'est un rectangle" ou " ABCD est un rectangle mais c'est un carré ", c'est donner trois informations : ABCD est un carré, ABCD est un rectangle et l'énonciation présuppose qu'il y a un sujet qui donne son point de vue et qu'il a les moyens de l'affirmer ;
- Formuler "ABCD est un rectangle mais c'est un carré " introduit une notion subtile d'opposition et permet de penser que tous les rectangles ne sont pas des carrés. Cette formulation contenant le mot mais n'est ni tout à fait de la logique, ni tout à fait des mathématiques. Le mot mais introduit une nuance par rapport à une propriété qui est énoncée : " le quadrilatère ABCD est un rectangle".
Ces trois expressions sont typiques des pratiques langagières des mathématiciennes et des mathématiciens qui articulent un lexique spécifique et des formulations différentes.
En classe, la complexité se traduit souvent en difficultés
La complexité des usages de la langue vient du fait qu'il est très difficile d'expliciter le sens de chaque mot et de se demander comment une personne va l'entendre. Même pour un sujet qui est à l'aise en mathématiques, cela peut être ni clair, ni conscient. C'est le produit d'une culture des usages sociaux qui passe par des pratiques langagières.
En général, la complexité n'est pas synonyme de difficulté. Néanmoins, dans la classe, les élèves sont confrontés à la complexité des pratiques langagières disciplinaires qui se traduit souvent par des difficultés. C'est le cas avec l'usage de la préposition avec qui est très complexe en classe de mathématiques.
«J'interroge aussi les pratiques langagières (toujours autour du mot « avec ») dans l'institution scolaire au travers des études de manuels d'une part et de l'analyse d'un « incident » en classe d'autre part. Ce travail se place dans une réflexion plus globale sur le fait que les élèves découvrent en même temps les objets mathématiques (en général par un travail explicite avec l'enseignant) et la façon dont on en parle, sans que soit généralement interrogée cette façon de dire les mathématiques (pourtant indissociable de la façon dont on les pense), et, à terme, sur la façon de travailler cette dialectique en formation et / ou en classe.»(Hache,2015)Hache C.(2015). Pratiques langagières des mathématiciens, une étude de cas avec "avec". Petit x., 97, pp.27-43.https://hal.science/hal-01397401.
L'usage de la langue en classe emprunte beaucoup aux pratiques langagières des mathématiciennes et mathématiciens de métier. Emilie BaronBaron E. et Hache C.(2019). Expliquer, justifier, prouver, démontrer ?. Repères IREM 115, pp.35-52.https://hal.science/hal-03257977/file/115_article_762.pdf, enseignante en mathématiques observe que le terme démonstration issu du métier de mathématicien a plusieurs usages dans la classe :
- Pour des élèves de 6e/5e et dans les manuels de ces niveaux les termes justifier, prouver, démontrer, expliquer sont interchangeables et signifient à peu près la même chose ;
- Les enseignants sont bien conscients de la différence dans la définition de ces termes mais les usages peuvent être très différents. Pour tel enseignant expliquer revient à attendre de l'élève une activité qui s'apparente à une démonstration formelle, et pour tel autre enseignant cela revient à attendre que l'élève fasse le lien avec les connaissances enseignées.
Aux usages langagiers liés aux mathématiques peuvent s'ajouter des usages liés à l'enseignement.
Des leviers du côté des sciences du langage et de la didactique du français
C. Hache fait un parallèle entre les usages de la langue en classe de français et ce qui pourrait être envisagé en classe de mathématiques. Les enseignants de français sont amenés à aider les élèves à s'approprier les usages de la langue pour comprendre des textes ou pour les produire. En classe de français, comprendre les usages du langage passe par :
- un travail collectif et réflexif car comprendre comment les autres comprennent un texte favorise la compréhension ;
- une explicitation aux élèves des stratégies de compréhension, autrement dit « comment on comprend ? »Bishop M.F.(2018). Former à la compréhension, la suite... . Site du centre Alain-Savary. Lien vers l'article..
Pour apprendre à lire, parler et écrire des mathématiques, on pourrait :
- travailler sur des textes courts ;
- pour chaque élève, dire ce qu'il a compris de sa lecture et comparer avec les différentes interprétations des autres élèves ;
- identifier les points communs, les différences et se demander si cela était prévisible dans le texte.
La langue comme objet d'apprentissage en mathématiques : un exemple
Formuler oralement l'expression (-5) + (-12) – (-7) – (+20) + (+2), invite à questionner les façons de dire l'expression et les concepts qui y sont attachés.
Une formulation possible : « moins cinq plus moins douze moins moins sept moins plus vingt plus plus deux ».
(Classe 4e de Camille, REP+ Académie de Lyon)
Les questions que cela soulève : Utiliser le mot plus correspond-t-il au signe de l'addition ou au signe du nombre positif ? De même le mot moins correspond-t-il au signe d'une soustraction ou au signe du nombre négatif ? En quoi dire autrement l'expression peut-il permettre de mieux comprendre le sens mathématique de cette formulation ?
Par exemple on peut proposer une autre formulation du début de cette expression mathématique : « moins cinq ajouter moins douze puis soustraire moins sept »
Il apparait que proposer des tâches où la langue est un objet d'étude permet de travailler :
- la compréhension et la production de formulations ;
- le contenu mathématique.
Ce travail sur la langue permet de mettre en oeuvre un processus de matérialisation de la langueHache C.(2017). Lecture et écriture en didactique du français, questions pour la didactique des mathématiques. 19e école d’été de didactique des mathématiques organisée par l’ARDM. https://hal.science/hal-01646998/document.
Des pistes en classe pour matérialiser la langue
Formulation(s) d'une conjecture
 Cet exemple a été proposé en quatrièmeGroupe Léo-IREMs de Paris(2018). « Formulations et reformulations », in APMEP Au fil des maths. N° 528. https://afdm.apmep.fr/rubriques/eleves/formulation-leo-num/(Agrandir le texte ci-contre). Il s'agit de formuler collectivement le théorème de Pythagore. Ce n'est pas l'établissement d'une démonstration mais la formulation d'une conjecture (Une conjecture est une idée non vérifiée, fondée soit sur une probabilité, soit sur l'apparence, CNRTL)
Cet exemple a été proposé en quatrièmeGroupe Léo-IREMs de Paris(2018). « Formulations et reformulations », in APMEP Au fil des maths. N° 528. https://afdm.apmep.fr/rubriques/eleves/formulation-leo-num/(Agrandir le texte ci-contre). Il s'agit de formuler collectivement le théorème de Pythagore. Ce n'est pas l'établissement d'une démonstration mais la formulation d'une conjecture (Une conjecture est une idée non vérifiée, fondée soit sur une probabilité, soit sur l'apparence, CNRTL)
Les élèves ont manipulé à l'aide d'un logiciel de géométrie des triangles rectangles et identifié les liens célèbres entre les carrés des côtés d'un triangle rectangle. On leur demande de proposer plusieurs formulations et de les compiler dans une liste.
Les élèves sont amenés à discuter une proposition choisie dans la liste. Petit à petit, soit à l'initiative de l'enseignant qui pose une question, soit avec une remarque d'un élève, on stabilise une proposition qui sera écrite dans la leçon. C'est une activité exigeante qui demande un temps long, soit 40 minutes dans l'expérience rapportée.
Formulation(s) d'une définition
Cet exemple a été proposé en sixièmeHache C. (2017).Fiche pédagogique élaborée par le groupe « Léo, langage, écrit, oral » de l'IREM de Paris.p.17-19. http://docs.irem.univ-paris-diderot.fr/up/Leo-FP-Reformulation.pdf. Il s'agit de formuler une définition de la médiatrice.
Après avoir manipulé sur un logiciel de géométrie la fonction médiatrice, les élèves sont amenés à identifier ce qui est invariant en modifiant la position des extrémités du segment initial. Les élèves identifient que la médiatrice passe par le milieu du segment et lui est perpendiculaire.
Les élèves sont invités à écrire une définition de la médiatrice, seul et en petit groupe. Puis une série de définitions est débattue collectivement. Les élèves ont la responsabilité d'écrire la définition qui apparaitra dans le cours.
Formulation(s) d'une démonstration
On peut faire le même type de travail avec une démonstration en mathématiquesBarbin E., Laborde C., Houdebine J., Giorgiutti I., Duval R. & Al.(1998). Produire et lire des textes de démonstration. Publications de l'Institut de recherche mathématiques de Rennes.http://www.numdam.org/issues/PSMIR_1998___S4/ .. L'idée est de travailler de manière dialectique la lecture et l'écriture d'une démonstration. Bien qu'au premier cycle il n'y ait pas de texte de démonstration, on peut démarrer avec des textes courts de trois lignes avec un contenu mathématique.
Formulation(s) d'un programme de construction
Dans le cas de programme de construction en géométrie, on peut travailler la restauration de figures, des figures téléphonées :
- les élèves écrivent un programme individuellement ou en petit groupe et après discussion collective, on décide d'un programme de construction ;
- par un jeu de "bouche-à-oreille" un élève communique son programme à partir d'une figure et après discussion collective à un autre qui réalise la figure, ils se mettent d'accord sur un programme de construction commun. Enfin, collectivement on détermine le programme de construction le plus efficace.
Dictée(s) en mathématiques
On peut transformer les exercices de formulation en dictée. Par exemple, l'enseignant dicte d'une certaine manière un calcul, et fait discuter les élèves sur une autre manière de dicter. Ou à l'inverse, dire ou écrire au tableau une expression mathématique et demander aux élèves comment ils dicteraient la formulation. Ce travail peut s'inscrire dans des rituels que les enseignants mettent déjà en place.
«Le travail ainsi mené en mathématiques sous forme de « questions flash » régulières ouvre une possibilité pour les élèves de questionner les usages langagiers en mathématiques : façons de dire, façons de noter, façons de prononcer des symboles, etc. Les questions ne sont pas toujours simples (nos usages ne le sont pas toujours !), mais la réflexion menée, la prise de recul initiée, le fait qu’elle soit menée explicitement, collectivement, apporte beaucoup.»(Hache et alii, 2018)Hache C. & alii.(2018). Dictée en cours de mathématiques ?. https://hal.science/hal-02292618/document.
Formulation(s) en langues étrangères
 On peut s'intéresser à la formulation des mathématiques dans d'autres langues. Par exemple pour la formulation du calcul (-12) – (-7), en anglais il y a une différenciation pour dire le signe "-". On utilise minus pour soustraire et negative pour le signe "-" du nombre. Toutefois des responsables du site MathsMonde hésitent sur l'usage effectif de ces dénominations dans la réalité des classes anglaises. Que ce soit en langue française ou en langue anglaise, il est plus compliqué de formuler une expression symbolique. Cela est dû aux structures grammaticales et à la conjugaison dans ces langues.
On peut s'intéresser à la formulation des mathématiques dans d'autres langues. Par exemple pour la formulation du calcul (-12) – (-7), en anglais il y a une différenciation pour dire le signe "-". On utilise minus pour soustraire et negative pour le signe "-" du nombre. Toutefois des responsables du site MathsMonde hésitent sur l'usage effectif de ces dénominations dans la réalité des classes anglaises. Que ce soit en langue française ou en langue anglaise, il est plus compliqué de formuler une expression symbolique. Cela est dû aux structures grammaticales et à la conjugaison dans ces langues.
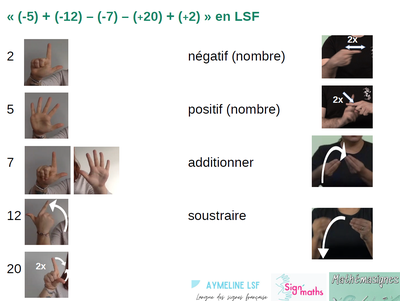
Pour la langue des signes, les mots et leurs usages sont différents pour le mot soustraire et le mot négatif. Leur usage est simple parce que les verbes ne se conjuguent pas (Agrandir le visuel ci-contre).
"2+2" et "2-2"
(Exemple simple de calcul en langue des signes par Christophe Hache)
Pendant 100 ans la langue des signes a été interdite en France, les mathématiques se sont développées sans elle. Des linguistes et des mathématiciens se sont intéressés à développer un vocabulaire spécifique pour la disciplineMillon-Fauré K.(2022).Plurimaths. La traduction des discours mathématiques en langue des signes. https://video.irem.univ-paris-diderot.fr/w/u7Ni2UYfSoyeb8GtME58bN.
Sur la chaîne Aymeline LSF (Langue des Signes Française), on signe la numération. Du fait que nos mains ont cinq doigts, la numération est centrée sur la base cinq. Cette représentation transforme notre façon de comprendre les nombres.
L'IREM de Toulouse et des linguistes de LSF ont formé un groupe de création de lexique mathématique Sign'Maths. Mathématiciens et spécialistes de la langue des signes débattent autour de diverses notions mathématiques, domaine par domaine, jusqu’à établir un signaire spécifique répondant à la fois aux contraintes linguistiques et aux critères mathématiques.
Sur la question des langues et langage en mathématiques , voir aussi …Ravez, C. (2024), Langues et langages mathématiques pour apprendre ensemble, dans Les mathématiques au centre du tableau. Dossier de veille de l’IFÉ, 147, février. p 16 à 18. ENS de Lyon. http://veille-et-analyses.ens-lyon.fr/DA-Veille/147-fevrier-2024.pdf |




