COMMENT METTRE EN OEUVRE LE PRESCRIT DES PROGRAMMES ?
| player1 | |
| L’énumération, une compétence infra didactique à enseigner explicitement ou dès la maternelle | 00:00:00 |
| Éléments de théorisation sur l’énumération | 00:12:15 |
| Dénombrer une compétence de haut niveau | 00:20:02 |
| Décompositions, recompositions additives | 00:24:08 |
L’énumération, une compétence infra didactique Intervention de J. Bernardin sur les compétences infra didactiques sur le site du CAS "des objets d'étude qui nécessitent un enseignement explicite" à enseigner explicitement dès la maternelle
J.Briand prend l'exemple de la note de service du 29 mai 2019 relative aux mathématiques à l’école maternelle.
Le rôle des programmes est de dire ce qu’il y a à faire dans la classe. Aujourd’hui, ils expliquent même comment il faut faire. J. Briand prend comme exemple l’énumération. Dans les programmes, « l’enfant doit maitriser la synchronisation du pointage des éléments de la collection avec la récitation des noms des nombres et apprendre à énumérer tous les éléments de la collection (pointer une et une seule fois, sans en oublier). Cette compétence d’énumération s’acquiert dans l’action, en dénombrant activement… ». Or pour le didacticien, l’énumération peut être indépendante du dénombrement.
La construction du nombre à l’école maternelle est le confluent de nombreuses activités. J. Briand propose une présentation de cette construction autour de trois dimensions : la situation d'action, des exemples de jeux et le savoir visé.
Pour contrôler une quantité, il faut faire en premier lieu un inventaire. Pour illustrer son propos, J. Briand présente une vidéo de moyenne section de maternelle. Dans la situation, un élève doit insérer une allumette et une seule dans chaque boite, sans possibilité d’ouvrir chacune des boites afin de vérifier s’il l’a remplie. Dans un premier temps l’élève n’organise pas ses boites et vérifie en les secouant. Or à l’ouverture, avec la maitresse, il se rend compte que plusieurs boites contiennent deux allumettes.
Après plusieurs séances, l’élève organise les boites dans lesquelles il a déjà inséré une allumette en les alignant devant lui. Il s’organise spatialement de façon à ce qu’il ait une exploration exhaustive d’une collection, et c’est cela l’énumération.
En formation, il est important de faire prendre conscience que plus les savoirs sont « simples » (notamment en école maternelle) et plus la consigne contient la solution.
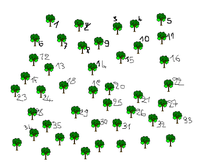 Plus tard, au CP, l’énumération peut être travaillée sur une feuille en demandant aux élèves de trouver le nombre d’objets dessinés.
Plus tard, au CP, l’énumération peut être travaillée sur une feuille en demandant aux élèves de trouver le nombre d’objets dessinés.
J. Briand prend l’exemple d’une élève qui écrit les nombres de la suite numérique à côté de chacun des arbres en respectant là une organisation précise, à savoir le sens de la lecture de gauche à droite et de haut en bas. Mais elle s’arrête à 35, alors qu’il en reste sur la feuille. L’enfant échoue alors qu’il dispose de la suite numérique et d’un procédé d’exploration relativement bien organisé. Il s’agit donc d’une absence de connaissance (que nous appelons énumération) qui se manifeste par une absence de synchronisation effective entre une connaissance numérique et une organisation conjointe de la collection et qui empêche d’effectuer l’inventaire de la collection (Briand 1993). Ce travail peut être fait également dans des salles de classe avec des objets sous des pots…
Éléments de théorisation sur l’énumération
Parmi les compétences observées pour effectuer un comptage, nombre d’entre-elles sont indépendantes du dénombrement (en italique dans la liste) :
- Être capable de distinguer deux éléments différents d’un ensemble donné.
- Choisir un élément d’une collection.
- Énoncer un mot nombre (« un » ou le successeur du précédent dans une suite de mot-nombres).
- Conserver la mémoire de la collection des éléments déjà choisis.
- Concevoir la collection des objets non encore choisis.
- Recommencer (pour la collection des objets non encore choisis) les quatre points qui précèdent tant que la collection des objets à choisir n’est pas vide.
- Savoir que l’on a choisi le dernier élément.
- Énoncer le dernier mot nombre.
« Dans certaines situations, l’élève a besoin de connaissances que l’école n’enseigne pas, mais qu’il doit pourtant mettre en œuvre pour apprendre le savoir ou pour utiliser ce qu’il a appris. »
Pour passer de la situation des boites d’allumettes à celle des arbres sur une feuille, il est possible de fixer les boites sur un support afin que les élèves ne puissent plus les manipuler mais ressentent le besoin de marquer, de signifier d’une manière ou d’une autre pour en faire l’inventaire puis à terme le dénombrement.
Dénombrer, une compétence de haut niveau
Le dénombrement est la capacité à produire une collection (C2) équipotente à une collection donnée (C1) sans voir cette collection au moment où l'on produit la collection (C2).
On peut dénombrer par subitizing, en comptant, numérotant, ou les deux en s'aidant d'images mentales, ou en ayant maitrisé le nombre.
Le comptage-numérotage est une pratique spontanée, qui peut être une procédure réussie de dénombrement mais sa manifestation ne garantit pas l'acquisition du concept de nombre (ni l'inverse). Alors quelles situations de comptage-numérotage mettre en oeuvre pour l'acquisition du concept de nombre?
J. Briand donne l'exemple du jeu des voitures et des garages qui consiste à aller chercher en un seul voyage le nombre d'objets nécessaires. Dans certains manuels, il est conseillé d'éloigner les deux collections uniquement pour les élèves les plus performants, comme si seuls ces élèves-là pouvaient résoudre ce type de problème. Il s'agit ici de rester très vigilants à la qualité des situations que l'on propose aux élèves.
Souvent caricaturée ou/et vue de façon superficielle, cette situation va permettre de passer du comptage numérotage au nombre dès lors que la modification du milieu d'apprentissage nécessitera de mémoriser l'information numérique à l'aide d'un écrit. Les situations proposées doivent faire évoluer le milieu d'apprentissage avec le passage à l'écrit pour aller vers la conceptualisation. L'évolution des traces écrites est un indice de l'acquisition de la maitrise des premiers nombres.
Décompositions, recompositions additives
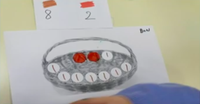
Le concept de l'addition peut être engagé lors de situations qui permettent de contrôler une quantité à l'aide d'un système de signes Grand N n°103. Pour illustrer son propos, J. Briand présente le jeu du panier. Cette situation consiste à aller chercher le panier correspondant au message donné ou à colorier les oeufs comme indiqué sur le message.
Pour que cela devienne une réelle situation d'apprentissage, il faut que l'organisation topographique des oeufs dans le panier ne corresponde pas au message. Par exemple, le message "4 bleus et 5 verts" doit être associé à un panier où les oeufs seront organisés avec 6 oeufs en haut et 3 en bas. L'objectif final est que l'élève réalise que 4 et 5 oeufs c'est égal à 6 et 3 oeufs.
Avec les élèves les plus fragiles, on garde des nombres plus petits et le matériel peut toujours ramener à une validation pragmatique.
Selon Vergnaud, la reconnaissance de la propriété de l'addition est une condition nécessaire à la conceptualisation du nombre.
Revenir au dossier "Manipulation: questions d'enseignement et de formation" en cliquant sur cette icône