SAVOIRS UTILES AU FORMATEUR POUR BIEN ACCOMPAGNER LES ENSEIGNANTS
| player1 | |
| Problème et situation d’apprentissage |
00:00:00 |
| Grille d’analyse pour le conseil en formation |
00:02:32 |
| Qu’est-ce que faire des maths ? |
00:03:54 |
| Observer le réel en formation |
00:05:04 |
| Mobiliser des connaissances pour construire du savoir mathématique: une nécessité |
00:08:53 |
Problèmes et situations d’apprentissage
L’équipe de J. Briand se réfère à la définition de Jean Brun (1990) Revue Math-École n°141, Institut de mathématiques (Neuchâtel)«Un problème est généralement défini comme une situation initiale, avec un but à atteindre, demandant au sujet d’élaborer une suite d’actions ou d’opérations pour atteindre ce but. Il n’y a problème que dans un rapport sujet/situation où la solution n’est pas disponible d’emblée, mais possible à construire. C’est-à-dire aussi pour un sujet donné peut ne pas être un problème pour un autre sujet, en fonction de leur niveau de développement intellectuel par exemple».
Un énoncé textuel de problème n’est pas un objet mathématique en soi mais un objet didactique.
Enseigner par les situations-problèmes est un mot-valise. Il est opportun de préciser tout cela en formation. En didactique des mathématiques, il s’agit non pas de se dire « Qu’est-ce que je vais enseigner ? » mais « Quel est le milieu que je dois créer pour que ce savoir visé soit acquis ou en voie d’acquisition ? ».
Dans la plupart des situations observées en classe, on peut dire que l’apprentissage se fait par familiarisation : l’enfant comprend le problème posé par le professeur ou le manuel ou le fichier et s’efforce de résoudre le problème ou de répondre à la question.
Dans la situation suivante : "Un enseignant montre à ses élèves 4 jetons dans une boite puis 3 dans une autre et met tous les jetons dans une seule et la ferme. Il écrit au tableau un 4 et un 3 et demande à ses élèves de prévoir à l’aide de signes combien il y a de jetons dans la boite" nous sommes en présence d'une situation d’une autre nature.
Il s’agit de construire des dispositifs adaptés à l’âge, aux connaissances, et aux intérêts des élèves concernés en se posant une question d’ordre didactique et une d’ordre plutôt sociologique :
- « De quels problèmes traiter dans ces dispositifs, le savoir visé est-il la solution optimale ? »
- « Comment s’assurer que les élèves voient dans ces activités des occasions d’apprendre ? »
Ces questions sont issues de la Théorie des Situations Didactiques développée par G. Brousseau.
Grille d’analyse pour le conseil en formation
En formation, l'installation d'un espace dialectique avec l’enseignant permet de lui donner les moyens d’analyser la situation. Pour cela quelques questions peuvent caractériser les situations :
- Y a-t-il bien un problème posé aux élèves ou ont-ils seulement à appliquer une consigne ?
- L’utilisation de la connaissance est-elle nécessaire pour parvenir à la solution du problème posé aux élèves ?
- L’élève peut-il comprendre la consigne et s’engager vers une solution sans disposer de cette connaissance entièrement élaborée ?
- Comment voit-il qu’il a réussi ou échoué ? (Est-il entièrement dépendant de l’adulte ou la situation comporte-t-elle des rétroactions interprétables par l’élève ?)
- La vérification du résultat peut-elle lui donner des informations sur la façon de réussir ?
- L’organisation de la situation permet-elle à chaque enfant d’être confronté au problème et de faire des tentatives ?
Qu’est-ce que faire des maths ?
« Faire des maths c’est construire un modèle donc du langage. »
La manipulation est nécessaire mais non suffisante dans les situations d’apprentissage. Elle doit permettre de prévoir puis de vérifier et ce dès la petite section de maternelle. Mais il y a besoin également de formules, de règles, de grammaire.
Il faut être vigilant en classe au fait que cette approche n’est pas réservée à une élite. Avec des élèves en difficulté, il faut revenir à ce genre de situation. Il est fait référence ici au rapport de la conférence de consensus du CNESCO sur l’individualisation.
Observer le réel de la classe en formation
J. Briand propose en formation de s’intéresser à un épiphénomène d’une ou deux minutes afin de regarder à la loupe un petit détail. Il montre une vidéo de classe qui permet de regarder toute la gestuelle associée à la parole, mais il est également intéressant de rentrer dans l’analyse par les verbatim.
La situation proposée se déroule en classe de CP : 9 lancers de dé ont permis, à chaque lancer, de mettre autant de jetons dans une boite tirelire. Au fur et à mesure des lancers de dé, l’enseignante écrit le résultat au tableau : 1 + 6 + 6 + 6 + 1 + 5 + 6 + 6 + 6. Il s’agit pour les élèves de prévoir combien de bonbons ils vont pouvoir obtenir en échangeant un bonbon contre 10 jetons.
Certains élèves commencent par avancer qu’ils ne peuvent pas avoir de bonbon car il n’y a pas de 10. Puis l’enseignante relance le débat en questionnant sur la possibilité d’avoir 10 jetons dans la boite. Et elle demande comment ils pourraient savoir s’il y a des paquets de 10. Une élève répond qu’il faudrait compter les jetons de la boite. L'ouverture de la boite permet de comprendre que des paquets de 10 peuvent être effectués. La relance du jeu est alors possible.
Mobiliser des connaissances pour construire du savoir mathématique : une nécessité
Cette situation permet de rentrer dans le champ de la réduction des suites additives. Pour accompagner les enseignants dans ce chantier, J. Briand propose de se poser la question non pas des savoirs en jeu dans cette situation mais bien des connaissances Marceline Laparra, Claire Margolinas, Les premiers apprentissages scolaires à la loupe. Approches anthropologiques et didactiques, De Boeck, 2016.
- Les connaissances sont tout ce qu’un individu met en œuvre pour réussir quelque chose c’est-à-dire que cela peut être du savoir mais également de l’implicite.
- Les savoirs sont tout ce qui peut se dire, tout ce qui peut se verbaliser.
Dans cette situation, la première règle qu’ils vont avoir à découvrir est "la liaison entre deux signes consécutifs permet de prévoir à l’aide d’un autre signe (oral ou écrit) le nombre de jetons obtenu à la suite de deux lancers". C’est-à-dire ici le signe +.
Cette règle permet de commencer à interroger leur première impression : « Il ne peut pas y avoir de 10 puisque c’est pas écrit. »
La deuxième règle est "la liaison entre deux signes, même non consécutifs permet de prévoir le nombre de jetons obtenus à la suite des lancers correspondants, indépendamment des autres lancers".
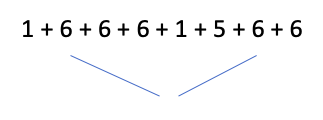
C’est une étape très importante pour l’élève, il est dans l’analyse d’un écrit.
La troisième règle est "une fois qu’on a pris un signe, on n’a pas le droit de le reprendre".
La quatrième règle "le résultat d’une liaison entre deux signes peut être signifié par un autre signe qui peut être combiné aux autres signes"
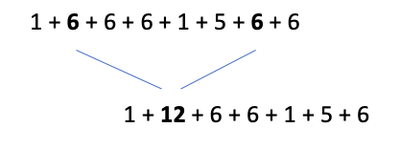
Ce sont ces connaissances que l’enseignant attend de voir émerger et il devrait construire ses interventions autour de cela. L’enseignant doit prêter attention aux connaissances qui émergent des élèves afin de les ériger en savoirs. Les savoirs sont plus facilement prévus, évalués, corrigés et enseignés que les connaissances. Or ce sont les connaissances qui génèrent les savoirs.
En formation, l’utilisation de courts extraits vidéo permet de se concentrer sur la micro-didactique et facilite l’entrée dans un cadre théorique plus large Petit x n°73 : la place de l’expérimentation.
La preuve par le langage
De récentes recherches ont démontré l’utilité du langage dans l’enseignement des mathématiques Rebière M., 2011, 16ème école d’été de didactique des mathématiques : « S’intéresser au langage dans l’enseignement des mathématiques, pour quoi faire ? ». Le langage, dans une situation d’apprentissage, permet la construction de savoirs.
Concernant la situation précédente, à terme l’ouverture de la boite sera considérée comme superflue. L’enseignant aura donc conduit les élèves vers l’élaboration d’un langage consistant lorsque les élèves manifesteront l’inutilité de l’ouverture de la boite. Dans les phases de validation, les énoncés produits dans la situation de formulation deviennent des théorèmes. Ils entrent à leur tour dans le milieu d’apprentissage. À ce stade, les écrits qui étaient d’abord descriptifs, constituent alors progressivement un milieu syntaxique de preuves. Petit à petit, le répertoire additif et la numération se construisent didactiquement.
Processus de mathématisation
Le milieu matériel ne peut à lui seul faire émerger le savoir mathématique. Chevallard (2004) énonce « Dans une mathématisation complète, on s’assure qu’un fait est vrai (ou pressenti) sur une base expérimentale puis on s’assure que, dans la théorie que l’on a bâtie par ailleurs, on peut déduire le fait en question. Cela mobilise toute une dialectique. » La théorie, on la bâtit ailleurs que dans le milieu matériel.
Pour conclure, en formation, il s’agit d’amener les enseignants à distinguer connaissances et savoirs, et à prendre en considération que « le cheminement d’un enfant, ce n’est pas la table des matières d’un bouquin ».
Revenir au dossier "Manipulation: questions d'enseignement et de formation" en cliquant sur cette icône





