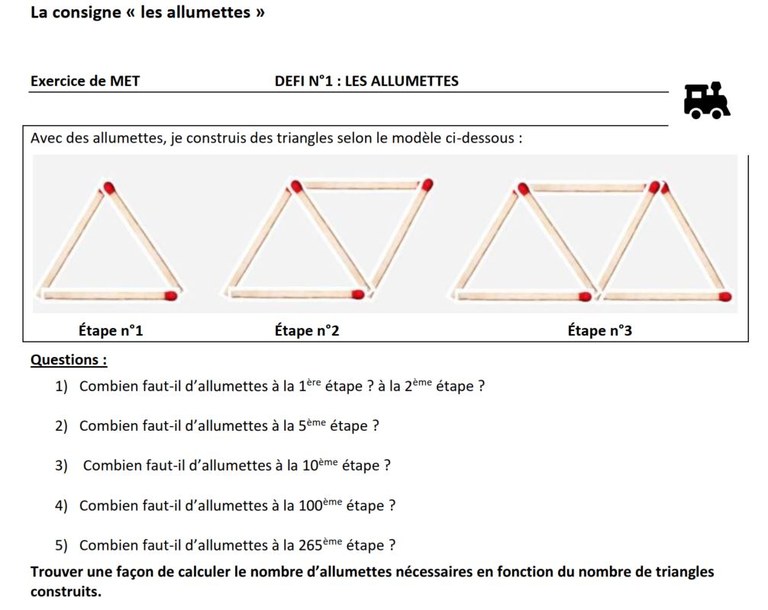
Une mise en commun lors d'une résolution de problème : La situation des "allumettes"
Le contexte
Mois d'octobre, l’extrait de la séance observée s’inscrit dans une organisation que l'enseignante nomme « Mise En Train »Martin-Dametto S., Piolti-Lamorthe C., Roubin S. (2012). TRAIN :Travail de Recherche ou d'Approfondissement avec prise d'INitiative. Bulletin vert de l'APMEP n°502.(nommée MET par la suite).
Le dispositif "Mise En Train"
Pour l'enseignante, une MET est un petit exercice de début d’heure déconnecté de la suite de la séance. Les MET sont de plusieurs types :
- MET-"phare" utilisée pour anticiper ou réinvestir une notion, par exemple des problèmes de proportionnalité ou de calcul littéral (introduction de la lettre et généralisation).
- MET-"Raisonner"
- MET-"Pétales de maths mentales", à l'initiative de l'enseignante, pour réinvestir des calculs mentaux, des petits problèmes de la vie courante ou des conversions.
L' extrait sélectionné correspond à l’introduction du MET-phare "calcul littéral", lors de la 1ère séance. Pour l'enseignante c'est une situation de recherche, elle a pour buts :
- de faire apprendre à chercher, ne pas être passif
- apprendre à communiquer
- convaincre autrui et se convaincre soi-même
- revenir sur ses erreurs.
- travailler collectivement à partir de propositions individuelles
Cette séance s’inscrit dans une progression de la MET-phare «calcul littéral » qui aboutit en milieu d’année à l’introduction de la lettre "x" en algèbre.
L'organisation des MET
Quatre temps spécifiques organisent cette MET :
- une passation de consigne avec toute la classe
- une recherche individuelle avec la possibilité de se déplacer pour prendre du matériel
- des échanges en petits groupes de trois-quatre élèves pour communiquer ses procédures
- une mise en commun des procédures des élèves avec toute la classe avec le tableau blanc comme support
La passation de la consigne de la MET "les allumettes"
Les préoccupations de l'enseignante : "Je m’assure qu’il n’y a pas de mots incompris, je le fais lire étape 1 étape 2 étape 3 pour bien différencier les trois schémas. J’essaye de regarder les élèves pour repérer une difficulté par rapport à la consigne. Je sais que je vais au moins faire participer six élèves différents. Je fais lire un élève mais systématiquement je relis la consigne, pour la redire à haute voix selon le niveau sonore et aussi pour être sûr qu’il n’y ait pas d’accroche sur les mots. On est avec un public d’élèves qui est en difficulté face à la compréhension de consignes, là je ne voulais vraiment pas que ce soit une difficulté, que la difficulté soit sur la recherche du nombre d’allumettes à telle étape."
Les attentes de l'enseignante : "L’idée c’est que les élèves explicitent leur méthode pour arriver à une formule, alors pas forcément une formule, cela peut-être une phrase qui expliquent comment ils ont fait pour calculer le nombre d’allumettes. Ce type de consigne, ils la retrouveront à répétition dans ces exercices dans mon introduction au calcul littéral. C’est pour ça que j’essaye d’insister sur une façon, une méthode, donner des synonymes pour tenter que ce soit clair pour eux"
Un extrait de la séance : la mise en communL’extrait donne à voir la mise en commun des procédures des élèves pilotée par l'enseignante (Transcription de l'extrait).
|
Les supports de la séanceL'enseignante propose un support papier sur lequel se trouvent des figures réalisées avec des allumettes. Les élèves écrivent sur leur cahier de mathématique dans une partie nommée "Calcul littéral" et ont la possibilité d'écrire sur une feuille blanche.
|
Le vécu de l'enseignante
L’extrait donne à voir les préoccupations, les buts, les étonnements de l'enseignante. player2
| player2 | |
| 1. J'ai envie qu'ils proposent eux-mêmes des erreurs | 00 : 00 |
| 2. Vous levez la main par contre je vais choisir | 01 : 39 |
| 3. Je ne m'attarde pas trop sur sa méthode | 02 : 27 |
| 4. Ça ne m'arrangeait pas à ce moment-là | 4 : 13 |
| 5. Là je dis "LA" réponse | 05 : 27 |
| 6. C’est la première fois qu’on me propose 2,5 | 08 : 02 |
| 7. J’avais pas du tout prévu ça | 10 : 45 |
| 8. Ça ne gênait personne dans la classe | 13 : 12 |
|
Titre |
Ce que dit l'enseignante
|
|---|---|
|
1. J'ai envie qu’ils proposent eux-mêmes des erreurs |
J’ai deux élèves du fond qui me disent qu’ils ont fait la même chose. Je leur ai dit de le mettre avec l’autre table. Je trouve intéressant qu’ils confrontent leur idée à quelqu’un d’autre. J’étais un peu coincée parce qu’ils se sont retrouvés un peu tous avec la même procédure. |
|
2. Vous levez la main par contre je vais choisir |
Je dis souvent ça aussi vous levez la main mais par contre je vais choisir dans quel ordre on va passer. Je sais qu’il y a plein de mains levées, des frustrations, et j'essaie de leur expliquer que si je choisis un ordre c’est qu’il y a une raison. Il y a une hiérarchie des propositions. J’espère que c’est une manière de ne pas trop les frustrer. Là il y a plusieurs élèves qui lèvent la main dont plusieurs élèves par table. En plus cela me laisse le temps de me dire eux ont fait ça. |
|
3. Je ne m'attarde pas trop sur sa méthode
|
Je ne m'attarde pas trop sur sa méthode. Mon intention là, c’est on obtient pas 20 allumettes comment on fait pour invalider et je renvoie aux autres. Là je pense que c’est du temps, l’heure commençait à bien tourner. Si j’avais eu le temps je lui aurais demandé qu’elle m’explique le lien entre “j’ajoute deux à chaque étape” et la multiplication par deux. Je sais que sur cette séance il y avait plein de choses et je n’avais pas le temps de tout regarder. Mais comme je sais que plus tard on reprendra ce genre de défi, on aura le temps de se reposer peut-être sur certaines procédures d’élèves. Mais là je sais que j’étais passée un peu vite, en fait je me suis dit ça va prendre du temps et il faut qu’on avance. Je pense j’avais en tête l’idée de se dire, faisons un schéma comptons et on va pouvoir voir que c’est faux. |
|
4. Ça ne m’arrangeait pas à ce moment-là |
Je me rends compte qu’on a pas traité la 5ème étape, ni la première ni la deuxième. ça ne me gêne pas parce que c'est l'élève qui m’a proposé de commencer ici. Un moment je me suis dit cela aurait pu gêner certains élèves qui auraient eu besoin qu’on valide les deux premières questions en fait, même si c’est du comptage. Il y a des élèves qui aiment bien avoir les réponses aux questions, donc je sais que cela m’a traversé l’esprit. J’étais embêté parce qu’il me proposait de passer à la suite mais moi je n’avais pas envie de passer à la suite, j’avais envie qu’on me propose autre chose que 20 allumettes. Cela ne m’arrangeait pas à ce moment-là. Surtout que lui commence à me dire en voulant passer à la quatrième question, bon ben voila, je passe à la suite |
|
5. là je dis "LA" réponse |
Là je dis la réponse, souvent ça ne gêne pas trop les élèves qu’il y ait vingt ou vingt et un. Je leur dis il y a deux résultats différents 20 et 21 ce n’est pas possible, c’est ce que j’ai dans la tête, je ne l’explique pas comme ça. C’est pas possible d’avoir deux résultats alors qu’est-ce que je fais? Il peut y avoir qu’une réponse possible. En schématisant on peut compter et on se rend compte qu’on a un résultat. Le schéma est utile pour vérifier par le comptage et aussi d’expliquer ce "plus deux" aux élèves, pour montrer le "dix fois deux plus un", expliciter la méthode. |
|
6. C’est la première fois qu’on me propose 2,5 |
Quand il m’a dit 2,5 je me suis dit ok, ça fait un moment que je fais l’exercice c’est la première fois qu’on me propose 2,5. J’essaye d’écrire lentement 2,5, j’essaye de faire le rapprochement, j’essaye de comprendre avant qu’il m’explique pourquoi "fois 2,5" J’ai le "fois 2", "2,5", "0,5". J’écris tout pour que les autres élèves réagissent; J'entends "je ne suis pas d’accord". Je me dis chouette, il va y avoir discussion, plutôt une discussion entre élèves, plutôt que ce soit moi qui dise que c’est faux. J’aime bien les entendre, dire je ne suis pas d’accord. Je me dis que cela va impliquer un débat, une discussion entre eux. Ça m’a donné l’impression qu’il improvisait la réponse. Je me rends compte que je m’attarde au nombre d’allumettes et pas au fait que le résultat de l’opération est faux. J’ai vu que quand j’écrivais, il faisait une drôle de tête, pas sûr de lui. C’était pas clair pour lui non plus. |
|
7. J’avais pas du tout prévu ça |
Là je me souviens j’étais contente, on va pouvoir enfin faire des petits schémas pour compter. Elle fait un triangle, elle fait ces triangles en pétales. J’avais pas prévu ça, je ne savais pas qu’elle allait faire ça. Je me suis dit on retourne en arrière, on avait fait un déroulé à l’étape 10. Le positionnement des triangles n’était pas clair, j’avais prévu d’utiliser les schémas au début, après on est parti sur autre chose. Je ne voulais pas que cela reste dans la tête d’autres élèves qui faussait la réponse aux questions. |
|
8. Ça ne gênait personne dans la classe |
J’étais super embêtée parce que cela ne gênait personne dans la classe, je regarde à gauche à droite, est-ce qu’il y en a pas un qui va réagir avant moi. J’aurais préféré que ça vienne de la classe, mais là on arrive à la fin de la séance. Si on avait traité en début d’heure les schémas on aurait pas eu ce problème. Au final il y a peut-être peu d’élèves qui se sont trompés dans la schématisation. |
Alexandra a été membre du LéA-Ifé réseau d'écoles et collèges Ampère, Lyon (2011-2020). La situation a été conçue dans ce cadre et est disponible sur le site PEGAME.
Revenir à la page d'accueil en cliquant sur cette icône :