Analyses de l'activité de l'enseignante et de l'activité mathématique

Dans l'extrait vidéo précédent, l’élève Lydia trace une figure au tableau différent de celles tracées au tableau par l'enseignante, indice d'un malentendu.

Quelle pourrait-être la nature du malentendu ?

• Première interprétation d’ordre socio-scolaire : L'élève importerait des énigmes sur les allumettes qu’on voit parfois posées sur internet dans un univers du quotidien dans l’univers scolaire : "faire une figure avec le moins d’allumettes possibles".
• Deuxième interprétation d'ordre socio-cognitif : L'élève reconfigure la tâche, d'un modèle de "proportionnalité" où le nombre d'allumettes est donné par 2x5, elle cherche alors à produire une configuration d'allumettes qui correspond à ce modèle.

Ces deux interprétations soulignent que cette tâche renvoie un problème "nouveau" par rapport à d'autres qui ont été fréquentées à l'école dans l'ordinaire de la classe. 

D'autres malentendus classiquement observés en éducation prioritaire sont à l'oeuvre dans cette situation :

• des brouillages de registres matériels et d'activité avec ce matériel ("deux petits bâtons là", " je dessine", "je surligne", "je stabylote", ... )
• Des malentendus  dans les verbalisations (numérotation des étapes versus numérotation des exercices,...).

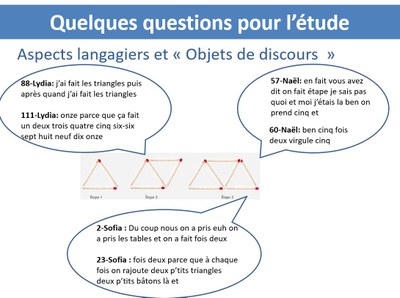
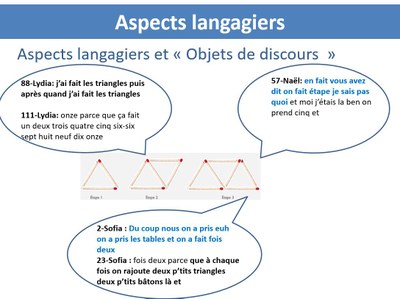
De quoi parle les élèves ? Quels sont leurs objets de discours ?

Ce qui est dit dans les trois bulles de la diapositive est assez emblématique des objets de discours mobilisés par les élèves dans la classe et qui sont source de nombreux malentendus :

• Concernant Lydia, son activité langagière et tant du côté de la représentation, du dessin du triangle en géométrie ("j'ai fait des triangles") que le dénombrement ("ça fait un, deux, trois...")
• Concernant Naël, son activité langagière se centre sur la  notion d'étape et dans l'univers du calcul ("cinq fois deux virgule cinq")
• Concernant Sofia, son activité langagière se centre sur le calcul ("on a pris les tables et on fait fois deux") et un discours intermédiaire entre l'univers des triangles (géométrie) et celui des allumettes (matériel).

La complexité de la tâche mathématique

• Lydia semble avoir compris qu'il fallait ajouter "plus deux à chaque fois". Cette formulation "on ajoute plus deux" plutôt que "on ajoute plus trois" indique qu'il y a quelque chose qui a été dépassé. Cela semble aller dans la bonne direction et en même temps ça n'aboutit pas.
• Concernant Matisse, il dit ''au début il y a trois allumettes''. Il va faire avancer la résolution du problème, mais en même temps cette formulation porte en elle une connaissance différente de ce que dit Lydia. Matisse est le seul élève qui tranche un peu entre les résultats 21 et 20.
• L'enseignante y revient dans l'entretien d'auto confrontation, elle pensait que le 21 convaincrait tout le monde "C’est pas possible d’avoir deux résultats alors qu’est-ce que je fais? Il peut y avoir qu’une réponse possible". Et Matisse est le seul élève qui vient essayer d'argumenter sur le résultat 21 "Il y a trois allumettes et après tu rajoutes un".

Les (re) formulations intermédiaires mobilisées par l'enseignante et les élèves
L'enseignante a écrit "10x2+1" soit "dix fois de plus un " pour obtenir 21 allumettes. La reformulation "dix fois deux plus un "de l'enseignante correspond partiellement à la conversion de ce que dit Matisse. Ce malentendu met au jour des connaissances en jeu qui ne sont pas élucidées.
Autrement dit, ces (re) formulations langagières traduisent des activités cognitives spécifiques et mettent au jour des difficultés auxquelles sont confrontés les élèves pour identifier les connaissances en jeu pour réaliser la tâche.

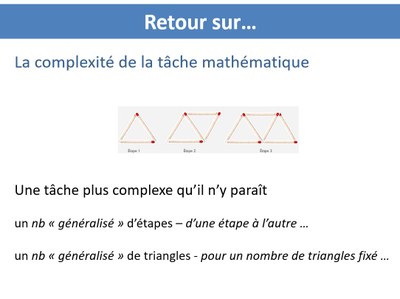
Une tâche plus complexe qu'il n'y paraît ...
C'est donc une tâche très compliquée, beaucoup plus que d'autres dans l'ordinaire de la classe. En effet tous les élèves savent dénombrer les triangles et écrire une série de calcul. C'est ce qu'ils font en permanence et pourtant, visiblement, ce n'est pas ce qui est attendu.

Qu'est-ce qu'on est censé comprendre ? Qu'est-ce qu'on est censé faire pour répondre à la question mathématique posée ?
Il y a quelque chose qui relève d'un processus de calcul généralisé qui soit nous permet de trouver le nombre d'allumettes en fonction du nombre d'étapes, ou soit en fonction d'un nombre de triangles fixé : Deux conceptions de la tâche radicalement différentes et qui sont source de malentendus dans les interactions.

ndlr : Lors de la formation de formateurs, on a eu beaucoup de difficultés à formuler les connaissances très précises qui sont nécessaires du point de vue des élèves pour accomplir cette tâche

La première conception "nombre généralisé d'étapes" (proche en partie de ce que dit Lydia) est une vision itérative

Description de l'itération : "à l'étape 1 je considère une allumette auquel j'ajoute deux allumettes, puis à l'étape 2, j'ajoute deux allumettes, à l'étape 3, j'ajoute deux allumettes, etc". Soit dans le registre symbolique 1+2+2+...+2, et dans le registre algébrique 1+nx2 ou 1+2n.

Dans le problème proposé dans cette situation, cette vision semble la plus accessible pour les élèves.

La deuxième conception "nombre généralisé de triangles fixé" est une vision fonctionnelle

Description fonctionnelle : J'ai un nombre de triangles constitués de trois allumettes chacun. Pour deux triangles adjacents il y a une allumette en commun. Il faut donc enlever les allumettes "redondantes". Or le nombre d'allumettes à retirer dépend lui-même du nombre de triangle.

On comprend que la vision fonctionnelle pour ce problème va difficilement aboutir car elle est très coûteuse à formuler. Ce n'est pas toujours le cas, par exemple pour le problème du "carré bordé" la vision fonctionnelle est plus facilement mobilisée par les élèves, alors que la vision itérative rarement, voir jamais.

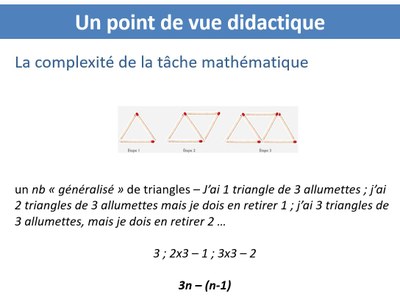
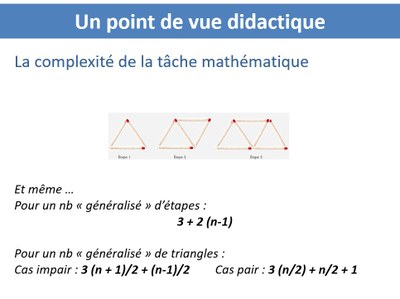
Et dans les deux conceptions itérative ou fonctionnelle, il y a de multiples manières différentes de procéder.

Par exemple, dans la vision itérative on peut avoir une autre démarche (proche de celle de Matisse)

Description d'une autre itération : "à l'étape 1 je considère trois allumettes, puis à l'étape 2 j'ajoute deux allumettes, à l'étape 3 j'ajoute deux allumettes, etc". Ce qui se convertit dans le registre symbolique 3+2+2....+2, et dans le registre algébrique 3+(n-1)x2 ou 3+2(n-1)

Description d'une autre approche fonctionnelle : On distingue les cas impairs et pairs de triangles. Pour un nombre impair de triangles on dénombre les triangles qui ont leur "pointe" vers le bas et les allumettes "planchers" soit 3(n+1)/2 allumettes par triangles pointés vers le bas et (n-1)/2 allumettes "planchers" ce qui donne 3(n+1)/2+(n-1)/2 allumettes. En raisonnant de la même manière pour un nombre pair de triangles on a 3n/2 +n/2+1 allumettes.

Bien qu'on puisse imaginer que des élèves pourraient s'engager dans cette conception, celle-ci a surtout l'intérêt de montrer que la tâche proposée est particulièrement dense en connaissances potentielles.

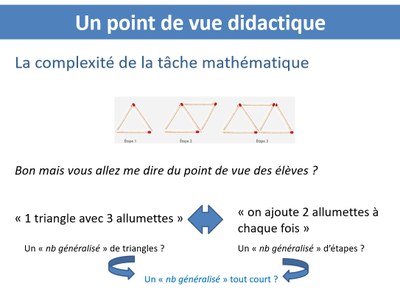
Les objets de discours sont fluctuants et circulent entre le nombre de triangles et le nombre d'étapes, sans que visiblement le nombre d'étapes devienne opérationnel.

La vision itérative est orientée par la formulation de la consigne ("Question 1 : combien faut-il d'allumettes à 1ère étape ? à la 2ème étape ?"). Dans cette formulation il y a une tension entre deux "démarrages" :

• par une allumette et on ajoute deux à chaque fois
• par un triangle de trois allumettes et on ajoute deux allumettes à chaque fois.

C'est deux démarrages itératif ou fonctionnel ("j'ajoute à chaque fois" ou "je prends un triangle") se confrontent en permanence dans les discours. Ce n'est pas productif car il faut se situer soit dans une vision itérative, soit fonctionnelle, et ce démarrage avec un triangle ne rentrent pas complètement dans la vision itérative.

Un malentendu qui génère des processus de calculs décrochés de la tâche

Quand on ne sait pas de quelle variable on parle, en termes d'étapes ou en termes de triangles cela se résout par la recherche d'un nombre "généralisé tout court". 

Cette tension entre ces deux visions permet d'éclairer l'activité cognitive de Naël quand il dit "l'étape je sais pas quoi", il serait sur le nombre de triangle mais il y a quelque chose qui ne se règle pas. Il s'inscrit dès lors dans un univers de calcul qui ne raccroche plus à la tâche et qui n'arrive plus à s'ancrer sur la modélisation de cette situation nouvelle.

C'est le cas de Naël, et c'est aussi celui de Sofia quand il dit " on a pris les tables et on a fait fois deux"

Reconfiguration de la tâche et fausses réussites

Quand Naël dit "ben cinq fois deux virgule cinq", on n'est passé dans une autre tâche complètement différente que l'on pourrait exprimer par "on a un nombre en entrée, un nombre en sortie et on cherche un processus de calcul qui permet de passer de l'un à l'autre" (par exemple " j'ai 5 triangles au départ et je cherche le calcul pour obtenir 11 allumettes"). C'est le cas de Lydia quand elle dit "on fait vingt fois dix".

Cette reconfiguration de la tâche mathématique interroge : cet élève a-t-il vraiment modélisé la situation ? On peut en douter et identifier cette reconfiguration de la tâche comme une fausse réussite au sens de J.P. Astolfi. 

Ceci peut expliquer pourquoi ces élèves qui proposent un processus de calcul décrochés du contexte ont tant de difficultés à argumenter pourquoi "deux fois dix plus un" ?

Un cas d'inversion de la tâche initiale

Lydia a dépassé que ce n'est pas "fois trois", mais sa procédure est toujours en lien avec un processus de multiplication. C'est le cas de tous les élèves qui ont basculé vers un "multiplier par deux".

Mais que cherche cette élève quand elle fait sa figure? 

• D'un côté elle trouve un ingrédient du modèle qui est "ajouté deux à chaque fois" et qu'elle modélise par "multiplié par deux le nombre de triangles". Cette erreur est partagée dans la classe.
• D'un autre côté elle inverse la tâche, elle prend son ingrédient "multiplié par deux " et cherche une figure géométrique dont la disposition des triangles serait adaptée (par exemple pour cinq allumettes elle dispose cinq triangles en "spirale" ce qui lui permet de valider 2x5=10 allumettes).  

il y a une vraie rationalité derrière ce que fait cet élève. C'est pour ça qu'elle résiste et semble finalement garder le lien avec la tâche initiale.

Des (re) formulations donnant lieu à des malentendus

Matisse parle sur les écritures produites par la maîtresse " 10 x 2 +1 ". Le "un" qu'il prononce essaye d'éclaircir l'écriture de ce "+1". Sauf qu'à aucun moment est écrit au tableau "trois allumettes et après tu rajoutes un".

On est peut-être dans la vision qui pourrait faire débloquer la situation, c'est à dire ce "un" et ce "trois allumettes". "Trois allumettes" qu'il faut regarder comme "une allumette auquel j'ai ajouté deux allumettes" dès la première étape. Mais ça n'aboutit pas et là, on voit une distance assez forte entre l'énoncé verbal de Matisse et la (re)formulation de l'enseignante.

Finalement ce qui est produit par l'enseignante comme reformulation ce " dix fois deux plus un" n'a pas réussi à éclairer pourquoi ce "10x2 + 1"

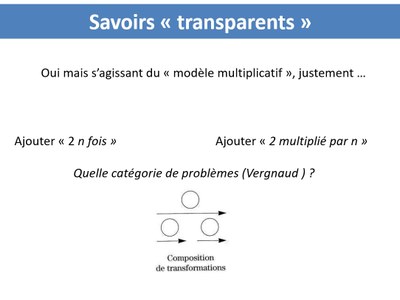
La structure conceptuelle (très complexe) de l'itération dans ce problème

(ndlr : dans cette partie Lalina Coulange mobilise les champs conceptuels de VergnaudG.Vergnaud(1990). La théorie des champs conceptuels, in Recherches en didactiques des mathématiques. La pensée sauvage, p.133-170)

Qu'est ce qu'il faut mobiliser comme catégorie pour la vision itérative ? 

• Ce n'est pas juste une transformation d'états où à partir d'un état initial on cherche l'état final. C'est la résultante d'une composition de transformations qu'est "ajouter deux", et encore "ajouter deux " et encore "ajouter deux" ,etc. "Ajouter plus deux à chaque fois"  appartient donc à la catégorie des compositions de transformations.
• Pour les élèves, ce n'est pas évident de faire le raccord entre "ajouter deux n fois" et "ajouter deux multiplié par n". Ce qui fait que ce problème est très compliqué et complètement inédit.   
• La composition de transformations additives est un savoir qui n'est pas facile à identifier car invisibilisé par l'institution. En effet la catégorisation du problème additif est pris en charge dans le premier degré qui en a une bonne connaissance et dans le second degré, on considère que c'est réglé et donc devient invisible.

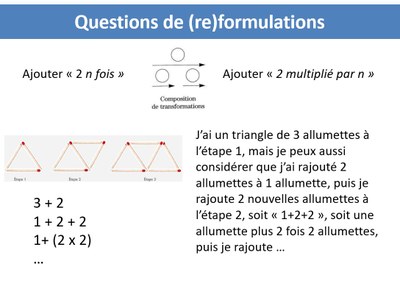
Des pistes pour produire des formulations intermédiaires

Essayons à partir de la formulation de Lydia qui dit "j'ai ajouté plus deux à chaque fois" en le convertissant dans d'autres systèmes de signes, c'est à dire faire comprendre ce passage délicat "j'ajoute deux et j'ajoute encore deux" une fois en  "j'ajoute deux" deux fois.

Je peux utiliser le discours " J'ai ajouté deux nouvelles allumettes à l'étape deux", soit "un plus deux plus deux". Soit "une allumette plus deux fois deux allumettes". Je peux l'accompagner avec des écritures symboliques. Je peux le faire avec des dessins puis montrer en accompagnant mon discours, peut être en rajoutant d'ailleurs des couleurs, en cachant des parties pour illustrer ce qui se passe dans le processus

Ces formulations intermédiaires pourraient servir de levier à entrer dans cette pensée itérative. Faut-il avoir élucidé les connaissances qui faisaient défaut ou qui bloquent ou qui sont compliquées à négocier dans la situation (ici la composition de transformations additives).

Penser le rôle du schéma comme un signe co-existant avec d'autres

Le rôle du schéma est problématique pour la situation, en effet quand :

• Le schéma produit le résultat, c'est le cas de Lydia qui dénombre les allumettes sur le schéma. Comme le but du problème est la recherche d'un processus de calcul qui va se généraliser, il va falloir abandonner le dénombrement à un moment donné. Dans ce cas-là, le schéma devient trop coûteux à mobiliser. 
• Le schéma permet de vérifier un résultat trouvé par un calcul, c'est le cas de Naël quand il mobilise la procédure "un nombre en entrée, un nombre en sortie" et aboutit à de fausses réussites.

Dans ces deux cas, le rôle du schéma ne paraît pas régler la situation.

Une piste possible c'est de penser le schéma comme un signe qui doit co-exister avec d'autres pour organiser, orchestrer la construction de cet exercice. Ce qu'on voit dans la classe, c'est qu'il prend difficilement ce rôle. Peut-être aussi parce que les connaissances en jeu sont difficilement identifiables. 

Pour (ne pas) conclure

Cette situation de classe représente un vrai défi en formation : analyser les savoirs transparents nécessaires pour réaliser la tâche prescrite par l’enseignante.

Pour s’exercer à cette activité très exigeante, on peut commencer par identifier des difficultés observées dans l'activité des élèves à produire des formulations et aux difficultés de l’enseignante à les reformuler. Puis remonter à l'analyse de la tâche afin de mettre au jour les savoirs en jeu.

Partir des malentendus, des formulations intermédiaires, de la diversité des inégalités socio-cognitives des élèves, c'est se donner des objets de travail du point de vue didactique dans l'accompagnement et la formation.