Cadres et registres de représentation sémiotique
cadres et registres de représentation sémiotique
Raymond DuvalDuval R. (1993). Registres de représentation sémiotique et fonctionnement cognitif de la pensée dans annales de Didactique et de Sciences Cognitives. IREM de Strasbourg. https://mathinfo.unistra.fr/websites/math-info/irem/Publications/Annales_didactique/vol_05/adsc5_1993-003.pdf, didacticien des mathématiques, propose les notions de cadres et de registres de représentations sémiotiques. Celles-ci permettent d'outiller la description et l'interprétation de l'activité mathématique d'un sujet ou d'un collectifDuval R.(2001). Comment décrire et analyser l'activité mathématique ? Cadres et registres. Université du Littoral, IUFM Nord Pas de Calais. http://tecfa.unige.ch/tecfa/teaching/LME/betrancourt/Duval2001.pdf .
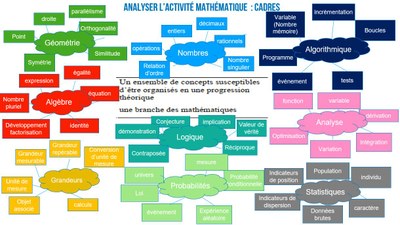
Cadres : concepts-outil et concepts-objetDans sa longue histoire, les mathématiques ont engendré un corpus de connaissances qui s'est structuré en "cadres" (Géométrie, Théorie des nombres, Algèbre, d'autres cadres sur la carte ci-contre). Un cadre est un ensemble de concepts susceptibles d’être organisés en une progression théorique. A l'intérieur de ces cadres, les concepts entretiennent des relations entre eux. Par exemple, le concept de symétrie axiale est un sous-concept de symétrie, lui-même sous-concept de transformation dans le cadre de la géométrie. Pour R. DouadyDouady, R. (1986). Jeux de cadres et dialectique outil-objet. Recherches En Didactique Des Mathématiques, 7(2), 5–31. https://revue-rdm.com/1986/jeux-de-cadres-et-dialectique/ par concept-objet, elle entend objet culturel ayant sa place dans un édifice plus large qui est le savoir savant à un moment donné, reconnu socialement. C'est l'énoncé d'un savoir scientifique qui peut être signifié dans différents registres de représentation. Le concept-outil est l'usage du concept pour résoudre un problème.
"Un élève, en activité mathématique, peut recourir à un concept-outil de manière implicite ou explicite [...] un élève a des connaissances mathématiques s'il est capable d'en provoquer le fonctionnement comme outils explicites dans des problèmes qu'il doit résoudre, s'il est capable de les adapter lorsque les conditions habituelles d'emploi ne sont pas exactement satisfaites, pour interpréter le problème ou poser des questions à leurs propos." (Douady,1986)
|
La carte ci-dessous a été utilisée en formation de formateurs pour illustrer quelques cadres issus des domaines des programmes de la maternelle au lycée, avec quelques concepts-objets associés. Cette carte peut-être utile pour amorcer une cartographie des concepts à partir d'une situation d'enseignement-apprentissage. Néanmoins elle ne suffit pas à déployer certaines dimensions :
|
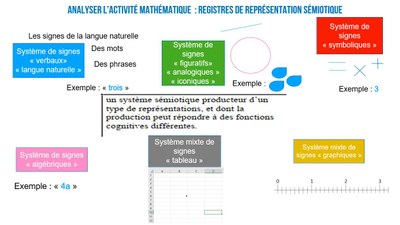
Registres de représentation sémiotique" « Représenter », c’est donner à voir, ou au moins rendre perceptible à la vue et à l’esprit [...] Il arrive enfin qu’on doive « représenter » des entités abstraites, qui n’ont pas d’autre mode d’existence que cette représentation : des nombres décimaux, des fractions, des fonctions, en un mot des objets mathématiques" (Document Eduscol, 2016) Les registres de représentations sémiotiques sont des productions constituées par l’emploi de signes appartenant à un système qui a ses contraintes propres de fonctionnement. Par exemple les "mots" sont des signes soumis aux contraintes de la langue, les "chiffres" sont soumis aux contraintes du langage symbolique du système de numération. Un registre de représentation sémiotique permet de représenter une facette d'un concept. Un registre est donc toujours partiel. Pour qu’un système puisse être un registre de représentation sémiotique, il doit permettre trois activités cognitives :
R.Duval souligne " L'importance des différents registres de représentation sémiotique utilisés en mathématiques " et pointe "les difficultés durables, souvent insurmontables, que créent les changements de registres exigés par l'activité mathématique. La compréhension n'émergeant chez les sujets qu'avec la coordination d'au moins deux registres de représentation, celle-ci devient un enjeu essentiel pour l'apprentissage des mathématiques." (Duval,1993) La «dynamique» propre à l'activité mathématique : de quelle nature sont les processus cognitifs en jeu ?Ce qui fait la spécificité de la recherche d'une solution d'un problème en mathématiques c'est qu'elle requiert des changements de direction de la pensée qui apparaissent comme des ruptures. Tout se passe comme s'il fallait brusquement changer la manière de représenter les données, ou penser à autre chose, à l'encontre du déroulement spontané du jeu d'associations qui a été induit par la première compréhension du problème ou les premiers traitements engagés. R.Duval note que "l'intérêt de la notion de «cadre» et de celle de «registre de représentation sémiotique» est de porter directement sur cette dynamique propre à l'activité mathématique, pour tenter de décrire avec précision les changements de direction de pensée qu'elle génère et pour en identifier les processus sous-jacents. " Ces changements de cadres et de registres induisent des changements de logiques de systèmes de signes, difficilement perceptibles par l'enseignant et plus encore par les élèves. Des questions pour aider à décrire l'activité mathématiqueR. Duval propose des questions directrices pour analyser l'activité mathématique :
Ces questions sont mobilisées dans l'analyse de la situation des "allumettes" |
La carte ci-dessous illustre cette notion de registre par des exemples. Cette carte a été utilisée en formation de formateur à propos de quelques représentations sémiotiques mobilisées dans la scolarité des élèves. Quelques points de vigilance sont nécessaires :
|
Revenir à la page d'accueil en cliquant sur cette icône :