Favoriser l'entrée dans l'univers des mathématiques, une question de langages ?
Les dimensions historiques et culturelles du point de vue du prescrit
Depuis la refondation de l'école de 2015, on observe une convergence et une cohérence des prescriptions autour de l’importance d’enseigner les dimensions culturelles et historiques des savoirs, en particuliers en mathématiques. Les termes « savoirs », « connaissance » et « culture » sont accompagnés de verbes comme « confronter », « enrichir », « mettre en perspective », « inscrire », « narrer » ou « dépasser un utilitarisme à courte vue ». Néanmoins l'enseignement des dimensions historiques et culturelles n'est pas sans poser des difficultés dans sa mise en oeuvre. En effet, cet enseignement passe plutôt par des formes de récits convoquant des mondes extra-scolaires qui ne sont pas les formes les plus caractéristiques de l'enseignement de la discipline, comme cela a été souligné lors de la session 4 "Apprendre et enseigner aux élèves allophones et itinérants: les mathématiques" au colloque international EVASCOLEVASCOL, Évaluation de la scolarisation des élèves allophones nouvellement arrivés (EANA) et des enfants issus de familles itinérantes et de voyageurs (EFIV), colloque international, avril 2018, coordonnée par Catherine Mendonça-DiasMENDONÇA-DIAS Catherine, enseigner des mathématiques avec des écoliers peu ou non francophones, Actes du 41ème Colloque international des Professeurs et Formateurs de Mathématiques chargés de la Formation des Maîtres (COPIRELEM), 2014
Dans le référentiel de l’éducation prioritaire
Dans l’introduction des programmes de mathématiques du socle commun au cycle 3La mise en perspective historique de certaines connaissances (numération de position, apparition des nombres décimaux, du système métrique, etc.) contribue à enrichir la culture scientifique des élèves. Dans l’introduction générale du cycle 4Ils utilisent des outils qui leur permettent d’être efficaces dans leurs recherches. Mieux comprendre la société dans laquelle ils vivent exige aussi des élèves qu’ils s’inscrivent dans le temps long de l’histoire. C’est ainsi qu’ils sont davantage confrontés à la dimension historique des savoirs mais aussi aux défis technologiques, sociétaux et environnementaux du monde d’aujourd’hui. Dans le rapport Villani-TorossianRappelons enfin que les mathématiques font partie de notre patrimoine culturel. Elles constituent l'une des plus anciennes et des plus nobles traditions intellectuelles de l'humanité.[…]En tirant parti de l’histoire des mathématiques, les professeurs inscrivent leur enseignement dans l’évolution de la pensée. De plus, les élèves sont souvent sensibles à la « légende des mathématiques ». La narration peut jouer ici un rôle motivant. D’autre part, les leçons épistémologiques qui se dégagent de l’histoire (rôle des problèmes, enchevêtrement des concepts et des techniques, nécessité de l’abstraction) sont évidemment de nature à contribuer à la formation, notamment en permettant de dépasser un utilitarisme à courte vue. |
 Les enseignants pratiquent l’usage des récits en mathématiques
Les enseignants pratiquent l’usage des récits en mathématiques
Les récits circulent dans la classe de mathématiques car toutes les pratiques enseignantes sont situées et contextualisés. Elles sont empreintes d’une certaine culture, que ce soit dans la langue et les langages utilisés (par exemple les nombres ne sont pas nommés ou écrits de la même manière dans différents pays), les écritures symboliques utilisées, la forme des problèmes, les récits qui les accompagnent, etc. Dominique Lahanier-ReuterLAHANIER-REUTER Dominique, Récits dans la classe de mathématiques, Equipe THEODILE dans Pratiques n°133/134, 2007 montre qu’il y a différents récits prototypiques dans la classe de mathématiques (cela ne date pas d'aujourd'hui comme le montre l'illustration ci-contre, extrait d'un manuel d'arithmétique de classe de fin d'études, rédigé par des inspecteurs généraux de l'instruction publique et primaire de la Seine, Ch. Pugibet, A. Adam et P. Gascon aux éditions Armand Colin en 1955). Elle distingue trois formes de récits:
- Celles qui organisent les faits mathématiques
- Celles qui convoquent le monde de la classe
- Celles qui convoquent des mondes extra-scolaires.
Ces types de récits peuvent être en tension entre eux mais aussi avec le discours explicatif. Toutefois les frontières entre ces formes de récits sont poreuses. Ces formes se déclinent selon que la production soit orale ou qu'elle soit écrite et peuvent-être produites par les enseignants ou par les élèves (dans l'illustration ci-contre on distingue deux types de récits écrits, l'un convoquant un monde extra-scolaire qu'est le réseau ferré et les horaires des trains et un récit qui organise des faits mathématiques sur la manière d'opérer avec les nombres dits "complexes", à remarquer aussi que la grandeur temps elle-même est l'objet d'étude).
Le tableau suivant synthétise cette typologie:
| Récits oraux | Récits écrits | |
|---|---|---|
| Des récits organisant des faits mathématiques |
|
 Les récits écrits produits par les enseignants qui inscrivent chronologiquement des actions évoquées et mettent en succession des événements s’inscrivent toujours dans une soumission au texte démonstratif. Ces récits tendent à disparaître avec le niveau d’étude (Dans l'illustration ci-dessus un exemple déjà cité de "chronique d'opération" sur les nombres dits "complexes" ou par exemple un enseignant qui écrit "Pour mener de A une parallèle à x'x, nous mènerons d'abord de A une sécante arbitraire AB, qui coupe x'x en B. Puis nous construirons sur AB un angle de sommet A etc.") Les récits écrits produits par les enseignants qui inscrivent chronologiquement des actions évoquées et mettent en succession des événements s’inscrivent toujours dans une soumission au texte démonstratif. Ces récits tendent à disparaître avec le niveau d’étude (Dans l'illustration ci-dessus un exemple déjà cité de "chronique d'opération" sur les nombres dits "complexes" ou par exemple un enseignant qui écrit "Pour mener de A une parallèle à x'x, nous mènerons d'abord de A une sécante arbitraire AB, qui coupe x'x en B. Puis nous construirons sur AB un angle de sommet A etc.") |
|
|
 Les récits écrits produits par les élèves qui organisent des faits « purement mathématiques », comme la construction d’une figure en géométrie révèlent une forte tension entre récits des actions et descriptions des contraintes. Par exemple Mathilde au CM1 écrit "On trace un cercle, puis on fait un point au centre du cercle, ensuite on trace une croix à l'aide du point et pour terminer on trace un losange à l'aide de la croix et du point. Le losange doit mesurer 2,8 de chaque côté." Les récits écrits produits par les élèves qui organisent des faits « purement mathématiques », comme la construction d’une figure en géométrie révèlent une forte tension entre récits des actions et descriptions des contraintes. Par exemple Mathilde au CM1 écrit "On trace un cercle, puis on fait un point au centre du cercle, ensuite on trace une croix à l'aide du point et pour terminer on trace un losange à l'aide de la croix et du point. Le losange doit mesurer 2,8 de chaque côté." |
|
| Des récits convoquant le monde de la classe |
|
 Les récits écrits produits par les enseignants sont de type « mémorisation » et ils sont quasiment absents. Par exemple dans un manuel on lit « nous venons de montrer qu’il existe une infinité de triangles semblables… ». Les récits écrits produits par les enseignants sont de type « mémorisation » et ils sont quasiment absents. Par exemple dans un manuel on lit « nous venons de montrer qu’il existe une infinité de triangles semblables… ». |
|
|
|
|
| Des récits convoquant des mondes extra-scolaires |
Soit des récits complets inspirés de l’histoire des sciences et des techniques comme par exemple celui de l'histoire de l’invention du compas. Les fonctions de ces deux types de récits sont différents: Les premiers le sont pour une mise en œuvre d’une modélisation quant aux seconds, ils le sont dans l’appropriation de la dimension culturelle des mathématiques. En revanche il partage le fait d’être des récits simplifiés et adaptés « transposés en objets scolaires » |
On trouve des récits « d’histoire des mathématiques » de façon systématique dans les manuels. Certains s’apparentent aux récits « anecdotiques » par exemple « la vie des hommes célèbres » et d'autres sont des récits « scientifiques » construits à partir de documents historiques PECH Marie-Anne, Utilisation des textes historiques en mathématiques à l’école élémentaire, mémoire de master, 2013. On trouve aussi des récits originaux sous forme de contes où les contenus mathématiques s’insèrent en tant que résolutions de problèmes que rencontrent les personnages. Par exemple la mise en oeuvre d'une séquenceBONNET Nicole & OUDON Élisabeth,"la malédiction des maths" en CM1/CM2, article sur le site de l'APMEP, 2007 de résolution de problème sur l'album de jeunesse "La malédiction des maths" en CM1/CM2. |
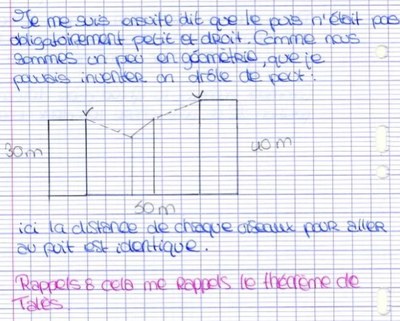
 Les récits oraux produits par les élèves sont sollicités par les enseignants. Ce sont des récits à partir d’énoncés ou inversement, ce sont des récits sous forme de « conférence », le dénouement de l’histoire est mathématique. C'est par exemple ce que décrivent deux élèves Yousra et Clémence en 4ème sur le blog de leur collègeNASSIT Yousra et PROMENAZ Clémence, "Les élèves deviennent professeurs pour une découverte des mathématiciens et leur théorème", blog du collège en REP+ Paul-Emile Victor, 2018. Les récits oraux produits par les élèves sont sollicités par les enseignants. Ce sont des récits à partir d’énoncés ou inversement, ce sont des récits sous forme de « conférence », le dénouement de l’histoire est mathématique. C'est par exemple ce que décrivent deux élèves Yousra et Clémence en 4ème sur le blog de leur collègeNASSIT Yousra et PROMENAZ Clémence, "Les élèves deviennent professeurs pour une découverte des mathématiciens et leur théorème", blog du collège en REP+ Paul-Emile Victor, 2018. |
 Les récits écrits produits par les élèves sont très rares mais on trouve des cas de textes brefs comportant des données chiffrées mettant en scène des personnages génériques. Les récits écrits produits par les élèves sont très rares mais on trouve des cas de textes brefs comportant des données chiffrées mettant en scène des personnages génériques. |
D.Lahanier-Reuter identifie trois tensions importantes :
- Différence entre récit oral et écrit
- Différence de « mise en scène » variées des récits
- En référence à la norme, c’est-à-dire les pratiques d’évaluations de ces différents récits.
La confrontation des élèves aux dimensions historiques et culturelles des mathématiques se situerait plutôt du côté des productions orales et écrites de l’enseignant qui convoquerait un monde extra-scolaire avec des tensions entre :
- La médiation orale ou écrite
- Les textes à déchiffrer, à étendre ou à valider
- L'anecdote ou le document historique et scientifique.
|
Sur la plateforme Néopass@action , thème 2 « Aider les élèves à travailler et à apprendre », des professionnels réagissent à une séance de mathématiques sur l’algèbre proposée par Claire, une professeure de mathématiques en collège. Dominique et Michel, enseignants experts expliquent que dans leurs classes, ils convoquent un monde extra-scolaire, précisément le contexte du métier de maçon pour évoquer l’utilité du théorème de Pythagore que Dominique renomme d’ailleurs "théorème des maçons". Cette discussion est particulièrement intéressante en ce qu’elle montre comment les questions mathématiques sont traversées par des aspects culturels. Le souhait de rendre les mathématiques accessibles à travers des récits, comme celui de Dominique et Michel est un trait que l’on retrouve chez de nombreux enseignants. C’est aussi le cas d’Isabelle en CE1/CE2 dans le thème 8 « débuter comme formateur, tuteur, conseiller pédagogique », elle convoque un monde extra-scolaire pour introduire la multiplication à travers un récit imaginaire, bref et amusant. |
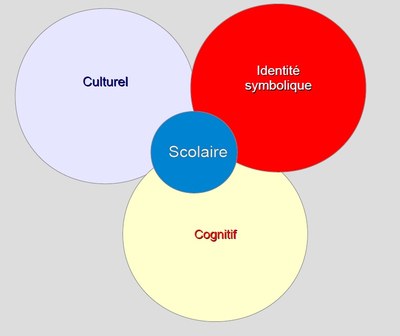 Par ailleurs, les recherches sous la direction de Patrick Rayou et Dominique GlasmanGLASMAN Dominique, RAYOU Patrick et Al., Qu'est-ce qui soutient les élèves ?2016 ont amené à structurer leurs observations à partir de différents « registres » qui contribuent aux apprentissages scolaires:
Par ailleurs, les recherches sous la direction de Patrick Rayou et Dominique GlasmanGLASMAN Dominique, RAYOU Patrick et Al., Qu'est-ce qui soutient les élèves ?2016 ont amené à structurer leurs observations à partir de différents « registres » qui contribuent aux apprentissages scolaires:
- Le registre cognitif relève des fonctions intellectuelles qui permettent d’apprendre, de réfléchir, d’élaborer, de construire selon des modalités propres à l'école (dans les écoles comme la nôtre, un style « rationnel-légal » qui impose de procéder par règles impersonnelles, un type particulier de rapport à l'écrit...).
- Le registre culturel est constitué de savoirs académiques et de connaissances générales sur le monde non réductibles à la sphère scolaire, mais donnant lieu tout autant à des classements et à des hiérarchisations.
- Le registre symbolique-identitaire est lié à ce que l’accès à un savoir requiert et construit un certain type d’identité personnelle et relie à une communauté pour laquelle il vaut et à laquelle l’élève est enjoint d'adhérer. Les travaux d'Yves ReuterREUTER Yves, le vécu disciplinaire pour comprendre le décrochage scolaire, 2017 sur le vécu disciplinaire peuvent éclairer ce registre en ce qui concerne les mathématiques.
Ces trois registres sont interdépendants et il est probable que la confrontation aux dimensions historiques et culturelles de la discipline permet de tisser des liens entre ces trois registres, mais comme nous l’avons vu au paragraphe précédent des tensions sont présentes dans l’usage de récits dans la classe.
Les langages au cœur de l’histoire et de la culture : Les « registres de représentations sémiotiques »
|
|
Raymond DuvalDUVAL Raymond, Registres de représentation sémiotique et fonctionnement cognitif de la pensée dans annales de Didactique et de Sciences Cognitives, IREM de Strasbourg, 1993, didacticien, a identifié plusieurs registres de représentations sémiotiques pour travailler sur un objet mathématique (nombre, fonction, vecteur,…).
Un lien sur notre site pour aller plus loin: Cadres et registres de représentations sémiotiques.
Michel FayolFAYOL Michel,L’acquisition du nombre, que sais-je ? p.19-35 et p.36-39, aux éditions PUF, 2012 décrit dans son ouvrage « l’acquisition du nombre », différentes représentations des quantités qui varient selon les cultures :
- Les codes analogiques (les doigts de la main, les bouliers et les abaques,…)
- Le code symbolique verbal (noms des nombres)
- Le code symbolique indo-arabe (les chiffres que nous utilisons quotidiennement pour écrire les nombres)
D'après M.Fayol, une question importante à trait au traitement cognitif des codes et trois perspectives sont défendues :
- Les individus mémorisent les procédures qu’ils ont employées et les entités sur lesquelles elles ont été appliquées. Ils les récupèrent mieux dans les situations nouvelles ressemblantes.
- Il existe des représentations abstraites dans lesquelles les formes seraient susceptibles d’être recodées, mais elles sont peu adaptées à l’acquisition du nombre, au moins jusqu’à la fin de la scolarité élémentaire.
- Le traitement numérique s’appuie sur trois types indépendants nommé « triple code » :analogique adapté aux traitements approximatifs, verbal, plutôt pour les faits arithmétiques, et visuo-spatial, privilégié pour traiter les chiffres arabes.
Des liaisons fonctionnelles relient chacune des représentations aux deux autres de manières indépendantes, en conséquence le passage d’un registre de représentation (par exemple les chiffres arabes) à un autre (dénomination orale) n’implique nullement de transiter systématiquement par l’interprétation sémantique, des transcodages directes (dits asémantiques) sont possibles.
Le centre Alain Savary propose des éléments pour une formation d'enseignants sur la notion de nombre décimal et sur la manipulation en mathématiques, en utilisant notamment des vidéos de l'école élémentaire JJ Rousseau d'Argenteuil et qui s'appuie en particuliers sur les registres de représentations sémiotiques.
Histoire et culture mathématiques, de quoi parle-t-on ?
|
|
L’approche épistémologique demande un rapport au savoir qui s’inscrit dans le temps et l’espace en prise avec une construction socio-politique des savoirs, ceux-ci étant ainsi recontextualisés. De ce fait, il semble nécessaire de constituer un corpus documentaire, qui n’est ni l’échafaudage de concepts, ni l’usage de techniques de résolution de problème, mais une médiation entre ces derniers. Cela correspond à l’histoire de la construction des savoirs mathématiques et de leurs usages. D'une part, cet aspect est, pour certains enseignants, complètement étranger et il est loin d’être évident de travailler à partir de documents historiques dans la classe. D’autre part, ce corpus n’est pas facilement identifiable, tant il est vaste, il n’est pas non plus toujours adapté en l’état et oblige à une mise en forme pédagogique et didactique, d’autant que les enseignants, formateurs, pilotes, premier ou second degré, n’ont pas forcément croisé, de manière institutionnelle, dans leur formation, la question de l’enseignement d’aspects culturels et historiques des mathématiques.
Néanmoins le travail en réseau prenant en compte les différents registres évoqués dans cet article, peut-être une clef pour trouver des compromis opératoires dans la mise en œuvre de stratégies pour confronter les élèves aux dimensions historiques et culturelles des mathématiques et les aider à accéder aux enjeux des savoirs enseignés par la médiation des langues et des langagesMAIRE-SANDOZ Marie-Odile, Une École inclusive : enjeux et démarches pour l’accueil et la scolarisation des élèves allophones nouvellement arrivés (EANA) , des élèves issus de familles itinérantes ou de voyageurs (EFIV), 2014.








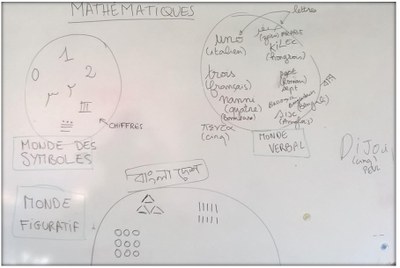 L’approche par les registres de représentations sémiotiques se traduit par des outils que l’on peut mettre en œuvre avec les élèves. Dans cette illustration un travail est mené avec des élèves dans un dispositif UPE2A-NSA
L’approche par les registres de représentations sémiotiques se traduit par des outils que l’on peut mettre en œuvre avec les élèves. Dans cette illustration un travail est mené avec des élèves dans un dispositif UPE2A-NSA Sur le
Sur le