- Outillage conceptuel, méthodologique et technique
-
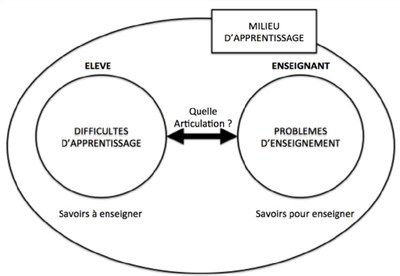
Des modules de formation de 2h ou 3h concernant des questions relatives à l'enseignement des mathématiques en maternelle et au delà sont proposés dans cette rubrique. Pour le centre Alain-Savary, la formation continue doit donner des espaces et des temps disponibles aux enseignants afin de mieux comprendre la nature des difficultés ordinaires d’apprentissages que rencontrent les élèves. Elle doit permettre aussi de mieux comprendre les problèmes ordinaires d’enseignement auxquels sont confrontés les professionnels. Dans ces modules, les concepteurs ont essayé de "tenir les deux bouts" entre les savoirs à enseigner et les savoirs pour enseigner de façon à ce que ces temps de formation permettent de parler des difficultés réelles du travail des enseignants.
questionnaire en amont de la formation pour identifier quelques difficultés que rencontrent les enseignants dans leur contexte d'exercice
Proposer un questionnaire en amont de la formation est une façon de "ramener du réel" en formation et un moyen efficace d'enrôler les enseignants dans le travail proposé. Cela permet au formateur de montrer qu'il prend en compte la singularité des situations d'exercice des enseignants d'une part. Et d'autre part, grâce à un travail de catégorisation des réponses au questionnaire, il pourra montrer que les difficultés exprimées par les enseignants relèvent de problèmes de métier et non de problèmes de personnes, ce qui est rassurant pour les professionnels.
Le formateur pourra par exemple proposer les questions suivantes :
- Depuis quand enseignez-vous (en maternelle) ? Avec quel(s) niveau(x) actuellement ?
- Citer une difficulté récurrente que rencontrent, selon vous, les élèves en mathématiques.
- Citer une réussite, même modeste, dans ce que vous faites en mathématiques avec vos élèves.
- Citer une difficulté récurrente que vous rencontrez lorsque vous enseignez les mathématiques.
- Quels types de collaborations avez-vous avec les collègues de l'école sur les questions d'enseignement des mathématiques ?
Prendre en compte les préoccupations professionnelles des enseignants en formation
Le travail de recherche réalisé dans le cadre de la construction de la plateforme néopass@ction a montré qu'en fonction de leur expérience du métier les préoccupations des enseignants varient.
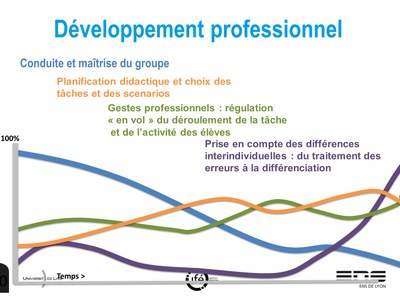
La question de l'ancienneté de l'enseignant dans le métier peut être un indicateur pour le formateur, lui permettant d'anticiper les systèmes de préoccupations majeures en lien avec les réponses apportées par le questionnaire. Le schéma du développement professionnel, ci-dessous, modélise les grandes tendances de l'évolution des préoccupations professionnelles dans le développement professionnel d'un enseignant. Ainsi des non-réponses à certaines questions peuvent être interprétées, non pas comme un refus de réponse mais comme un objet éloigné des préoccupations de l'enseignant.
Ressources à destination du formateur pour préparer le travail de catégorisation des réponses
Sur les obstacles et les difficultés d'apprentissage en mathématiques en lien avec les travaux d'André Tricot sur les Processus d'apprentissage (De 16min à 46min)
- Concepts mathématiques (Ex : Construction du nombre)
- Compréhension/langage (Ex : Compréhension, Analyser le texte d'énoncé, Manque de vocabulaire, Compréhension de l'énoncé)
- Procédures/savoir-faire/automatisation (Ex : Trier les données utiles, Mettre en oeuvre des stratégies, Transférer des démarches étudiées)
- Conceptualisation/prise de conscience des savoirs disciplinaires/secondarisation (Ex : Raisonnement, Abstraction, Privilégier la compréhension plutôt que la "réponse")
- Vécu disciplinaire (Ex : L'élève acte bien souvent qu'il est nul en maths)
Sur ce qui est difficile à enseigner pour les enseignants en lien avec les cinq focales de Roland Goigoux et les principes de fonctionnement collectif d'Yves Reuter
- Connaissances mathématiques et didactiques (Méconnaissance des objets d'apprentissage, Formation initiale littéraire, Manque de culture didactique)
- Différenciation (Étayer trop ou pas assez, Mettre en place une remédiation efficace, Adapter son discours aux besoins de chacun)
- Planification, outils, supports (Proposer des activités, Progressivité, Programmer les apprentissages, Des situations concrètes)
- Explicitation, accompagner la prise de conscience des apprentissages (Faire expliciter les élèves, Passage de la manipulation à la conceptualisation, Aider autrement qu'en donnant la stratégie)
- Coopération et entre-aide (Manque d'échanges, Pas assez de mutualisation entre nous)
- Modules de formation
-

Expliciter les consignes au cycle 1
Quelles consignes pour favoriser quelles activités cognitive et langagière des élèves ? Que faut-il expliciter ou laisser dans l'ombre ? Quels indicateurs langagiers (verbaux et non verbaux) prélever pendant la séance pour savoir si les élèves sont en train d'apprendre, savent déjà, sont encore loin des objectifs d'apprentissages ciblés ? Ce module tente de répondre à ces questions en analysant l'activité conjointe d'une enseignante de PS et celle de ses élèves.

Prise en compte des réponses erronées des élèves
Comment s'emparer des réponses erronées des élèves dans les situations d'apprentissages ? Pour en faire quoi ? Ce module de formation traite de la question des régulations didactiques au coeur des séances d'apprentissage au cycle 1.

Résolution de problèmes en MS
Ce module de formation propose d'analyser avec un groupe d'enseignants une pratique de résolution de problème en Moyenne Section. À partir d'une photo et d'un extrait vidéo, le collectif est amené à repérer dans ce que fait la maitresse, ce qui peut outiller les élèves pour construire du langage mathématique et structurer la pensée. Comment distinguer les buts de la tâche, des objectifs d'apprentissage ? Quels sont les "savoirs invisibles" qui sont nécessaires pour réussir la tâche ?




