Des supports mathématiques
Avertissement
Kevin Gueguen, auteur et propriétaire des fichiers qu'il a construit pour les maitres et maitresses de l'école élémentaire JJ Rousseau, accepte de les mettre à la disposition des formateurs et des enseignants qui le souhaitent, dans le cadre des conditions définies par une licence creative commons. Tels qu'ils ont été conçus, ces fichiers sont au nombre de cinq mais ne sont pas rattachés à un niveau de classe. Dans l'école chacune des 17 classes consacre une séance de 45 minutes par semaine au travail de résolution de problèmes en co-intervention enseignant/M+. A l'entrée au CP chaque élève commence à travailler sur le fichier de niveau 1, puis il avance à son rythme, accompagné par l'enseignant et le M+, pendant sa scolarité à l'école élémentaire. Cela signifie, par exemple, que dans une classe de CE2, quelques élèves, parce qu'ils sont allophones, récemment arrivés sur l'école et/ou peu scolarisés antérieurement, peuvent travailler transitoirement sur le fichier de niveau 1, tandis que d'autres, chacun avec son parcours et son vécu scolaire, travailleront sur les fichiers de niveau 2, ou 3 ou 4 voire même 5. Le choix assumé de l'équipe est de permettre à chacun de travailler et d'apprendre à son rythme dans ce temps spécifique.
Comment et pour quoi utiliser les fichiers de l'école JJ Rousseau
Consulter le document en ligne
Télécharger le document en PDF
Dans un document de 400 pages intitulé Mathématiques Résolution de problèmes, qu'il propose à la consultation et au téléchargement Le livret est téléchargeable dans le cadre des conditions définies par la licence Creatice commons ci-dessus Si vous souhaitez travailler à partir de ce document et que vous avez des interrogations, vous pouvez vous adresser à Kevin Gueguen à l'adresse suivante Kevin.Gueguen@ac-versailles.fr. Dans ce livret, Kevin Gueguen retrace la démarche scientifique et la mise en oeuvre pratique du projet de l'école autour de la résolution de problèmes du CP au CM2.Nous en avons extrait quelques éléments qui aide à comprendre le sens de la démarche.
La méthode
Ce document est un travail de synthèse, d’analyse et de méthodologie sur la résolution des problèmes du CP au CM2. La méthode, et ses supports, détaillée dans ce document est basée sur la catégorisation des problèmes additifs et multiplicatifs de Gérard Vergnaud. Cette méthode n'est pas une « méthode Vergnaud » mais une méthode originale et explicite d'enseignement/apprentissage des stratégies de résolution de problèmes par modélisation logique basée sur la typologie de Vergnaud. Ce projet permet de porter une attention très forte aux isomorphismes des problèmes. Par-delà la surface, c'est l'étude structurelle profonde qui est privilégiée pour maximiser les transferts.
Les schémas utilisés ont été créés par le maitre supplémentaire et sont l'adaptation de la représentation théorique des situations mathématiques. Une typologie détaillée couplée à une progression sur cinq années est proposée par le maître supplémentaire. Les documents méthodologiques sont également mis à disposition.
Ce projet est mené sur l’ensemble des 17 classes de l’école élémentaire Jean-Jacques Rousseau d’Argenteuil pour les années scolaires 2014-2015, 2015-2016, 2016-2017 et 2017-2018; il est inscrit dans le projet d'école. Il a débuté en 2012-2013 avec les classes de CE1, puis en 2013-2014 avec les classes de CP, CE1 et CE2.
Le projet pédagogique
"La pratique régulière que nous mettons en place vise à développer l'efficacité des procédures des élèves et leur automatisation. Cette automatisation « réflexe » est alors un outil permettant d'aborder avec plus d'efficacité les problèmes complexes (automatisation de multiples procédures connues) et les problèmes ouverts ( procédures par essais et analogies)".
L'équipe fait donc le choix assumé d'un enseignement explicite des stratégies de résolution de problèmes ( Problem Solving Teaching) plutôt qu'un enseignement basé sur la situation problème ( Problem Based Learning). Celui-ci ne saurait précéder le premier mais ces deux aspects ne sont pas opposés, ils sont articulés. « Je vais apprendre à faire puis j'apprendrais encore en faisant ».
C'est la rencontre répétée avec des situations problèmes variées qui permet l'émergence de réflexes cognitifs par l’utilisation d’une méthodologie adaptée. Nous entendons par « répétée » le fait de rencontrer ces situations chaque semaine durant toutes les années du CP au CM2. Le plus grand nombre de rencontres possibles est évidemment souhaité. Cet aspect doit être abordé à la fois qualitativement et quantitativement.
L'automatisation ne se fait pas sans réflexion ( complémentarité entre sens et technique), celle-ci se nourrit et grandit par l'acquisition de stratégies efficaces : une situation connue des élèves appelle une procédure connue, une situation inconnue que nous introduisons tendra à se rapprocher par quelques éléments de similarité d'une situation connue, qui appellera aussi des procédures connues qu'il faudra adapter, c'est ce que nous appelons le principe d'analogie. Cela nous pousse à expliciter et étudier profondément, autant que possible, le maximum de situations.
étapes et stratégies essentielles pour enseigner la résolution de problèmes
Nous détaillons dans ce chapitre les différentes étapes qui nous semblent nécessaires pour résoudre un problème arithmétique. Ces étapes prennent en compte la construction / la reconnaissance du schéma pour catégoriser les problèmes. Cette étape est essentielle à nos yeux pour que l'élève montre qu'il comprend la structure du problème ( sa « grammaire ») afin qu'il puisse signifier ce qu'il sait, les liens entre les éléments qu'il connaît et ce qu'il cherche. Cette structure permet d'établir une stratégie de résolution selon l'équation qui se met en place.
L'explicitation de la démarche de résolution est un point à ne jamais négliger. L'élève doit être amené à justifier ses choix, à expliciter sa démarche. Cela est nécessaire pour structurer sa pensée, ordonner des informations, apprendre à expliquer aux autres pour, si l'occasion se présente, développer le tutorat et la coopération.
Cette démarche vise à apprendre, petit à petit, à formaliser des raisonnements de plus en plus complexes. Nous pensons que nos élèves y gagnent pour la poursuite de leur parcours scolaire.
Étapes et stratégies essentielles
Les effets sur les performances des élèves
Il y a donc plusieurs facteurs de réussite.
- Le travail régulier avec une exigence forte en résolution de problèmes sur plusieurs années conduit au progrès de tous les élèves dans ce domaine. Il y a toujours des élèves qui ont des difficultés mais ils sont moins nombreux et les difficultés sont moins fortes.
- Un changement des pratiques en mathématiques se traduit par une amélioration notable des connaissances et compétences des élèves.
- Ces changements au niveau des pratiques se traduit par un travail différent concernant le calcul mental au quotidien, par une exigence plus élevé, par un changement de conception de l'évaluation au quotidien et par une plus grande prise en compte de l'importance du travail sur la mémorisation à long terme de faits mathématiques.
Les fichiers Les fichiers de résolution de problèmes sont téléchargeables dans le cadre des conditions définies par la licence Creatice commons.
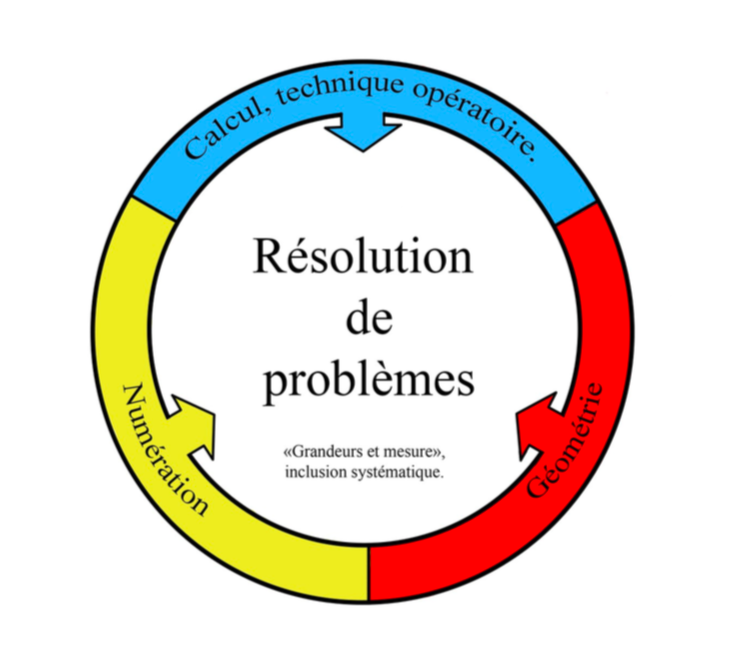
Dans notre projet la résolution des problèmes est mise au centre du domaine mathématique, entourée des outils qui vont permettre de la traiter avec efficacité. Cette démarche fait apparaître tous les entrelacs et ramifications entre les domaines étudiés. Ces outils sont nécessaires à l’élève et, parce qu'ils le sont vraiment pour lui (notion de besoin), l'élève s'en saisira d'autant plus ( un pari que nous prenons). L’élève est guidé et accompagné vers l’apprentissage efficace de ce qui lui est nécessaire pour avancer dans le projet.
Les supports destinés aux élèves et enseignants sont le fruit du travail du maître supplémentaire en collaboration avec des enseignants de l'école. Ce document a pour but de proposer une schématisation/ modélisation explicite des situations mathématiques rencontrées, de proposer une démarche de découverte et d'approfondissement progressive et spiralaire des différentes catégories de problèmes et de proposer des stratégies de résolution efficaces en étudiant la structure profonde des problèmes.
Il convient de garder à l'esprit que ce projet est conçu, pour être mené le plus efficacement possible, en co-enseignement même s'il est envisageable de mener des séances seul, par exemple avec une moitié de classe qui travaille en autonomie complète sur une activité qui le permet.
Ainsi, dans cet instant déterminé qu'est « la résolution de problèmes » certains points du programme peuvent être abordés individuellement avec les élèves les plus avancés avant une étude avec le groupe classe pour ensuite mobiliser des tuteurs. De même, certains points du programme ont pu être renforcés avec les élèves les moins avancés selon une logique spiralaire. Tous les domaines de maîtrise de la langue sont bien sûr mobilisés dans ce projet car la clarté de l'énoncé d'un raisonnement par l'élève est liée à la bonne conception de la démarche.

Cette œuvre est mise à disposition selon les termes de la Licence Creative Commons Attribution - Pas d'Utilisation Commerciale - Pas de Modification 4.0 International