Regard d'une didacticienne sur les vidéos de l'école d'Argenteuil

Par Patrick Picard — publié 16/01/2018 15:40, Dernière modification 03/12/2018 16:01

Dominique Lahanier-Reuter, du Laboratoire LACES de l'Université de Bordeaux, a participé au séminaire intermétier qui a analysé les vidéos de l'école élémentaire Jean-Jacques Rousseau d'Argenteuil. Elle a partagé son point de vue

Bandeau Reuter

Plusieurs points sur lesquels ancrer une réflexion.

Dominique

Une discipline scolaire au centre de cette méthode qu’ils disent employer

Cette démarche et ces dispositifs recentrent les pratiques de classe
autour d’une discipline scolaire unique, les mathématiques,
au travers de :

Les mathématiques, une discipline scolaire particulière

Dans notre recherche sur le vécu disciplinaire, nous avions pu construire une carte des mathématiques : les élèves éprouvent des sentiments extrêmes, amour ou haine, à l’égard de cette discipline. Cette haine est attribuée à l’absence de sens, à l’inutilité, aux difficultés rencontrées, à l’impossibilité d’utiliser certaines stratégies, à la peur ressentie, au langage particulier, à l’ennui, à la routine, à des exercices détestés : les problèmes d’arithmétique, à l’image de soi négative, à l’impossibilité de se voir changer, aux humiliations, à l’absence d’aide…

ses exercices emblématiques -les « problèmes arithmétiques »-,
ses pratiques langagières spécifiques -centièmes/centaines, parties/tout, chiffre/nombre, etc.-,
ses erreurs attendues - 43,15 > 43,8 ; 13 fois 3 c’est 13 x 13 x 13 ; aire/volume/périmètre etc.-,
les émotions qu’elle suscite -joie de la compréhension soudaine, désarroi de l’incompréhension,
etc.- (voir encadré ci-contre).

C’est donc une vision particulière de la discipline scolaire qui apparait ici et que nous tentons de décrire. Ceci a pour conséquence, puisque la trans/pluri/inter disciplinarité n’est pas l’objectif ou la structure dominante dans ces classes, que des références plus spécifiques à l’enseignement de cette discipline, à ses objets, à ses apprentissages… peuvent être convoquées pour mieux comprendre ces pratiques et leurs effets.

La « méthode Singapour », entre tradition et innovation

Nous avons posé la question "Que vient pallier la méthode de Singapour ?" à l'équipe de l'école élémentaire Rousseau

Les enseignants expliquent que ladite "méthode Singapour" (édition française) s'est accordée naturellement avec leurs pratiques de classe, il y a deux ans, car elle est en adéquation avec les outils qu'ils ont créés et sans cesse améliorés depuis cinq-six ans en résolution de problèmes. Marie explique "En fait tu t'aperçois que dans la résolution de problèmes, il nous manquait une partie et que c'est le même procédé et ça s'emboîte. Il nous manquait la partie numération et calculs au quotidien". David complète "C'est à dire que dans les exemples proposés par Singapour, on recrée des exercices en utilisant les schémas de résolution de problèmes". Marianne explique que de son côté "J'utilisais Brissiaud avant, qui marchait très bien [...] Les autres le (d'utiliser la méthode "Singapour") font et comme ça a bien marché, pour plus de cohérence il fallait que tout le monde s'y mette". Quant à Christophe, coordonnateur du réseau, il conclue la discussion sur ces mots "Je trouve intéressant de remarquer que la question porte sur Singapour mais que les réponses portent sur autre chose. [...] On parle de Vergnaud, des fichiers de Kevin et de la méthode de Singapour, mais ce qui ressort c'est la construction collective, qui s'est faite dans le temps, d'un outil aménagé, régulé, etc. Le levier, il est là. Il se trouve que ça fonctionne avec Singapour, et tant mieux, mais le levier, il est dans les mots utilisés : on se posait des questions, on a construit dans la durée, on régulait, on aménageait, on testait, etc."

Dans la revue Diversité revue à paraitre, Patrick Picard analyse : "La déferlante « méthode de Singapour » est présentée par le magazine Le Point comme ultime ressource contre les difficultés d’apprentissage des mathématiques en primaire. Pourtant, elle est largement construite à partir de connaissances empruntées aux didacticiens français qui expliquent depuis des décennies qu’il faut un important plan de formation pour développer les compétences des enseignants du primaire dans l’enseignement de la numération décimale ou des catégories de problèmes. L’idée n’est donc pas d’être « pour » ou « contre » telle ou telle « méthode », mais de comprendre à quelles conditions les outils qu’elle propose peuvent être, ou non, utilisables par des enseignants plus ou moins à l’aise avec la discipline enseignée. Devant l’augmentation de « tout ce qu’il y a à faire », « peu de professionnels peuvent réagir efficacement à toute cette complexité dans leur travail quotidien », explique Bryk. Ces observations suggèrent d’accorder encore plus d’attention aux environnements organisationnels qui façonnent la manière dont le travail est mené, plutôt que de croire à l’effet de telle ou telle mesure prise isolément. ». Dans l’enquête réalisée dans une école REP de Argenteuil, qui a décidé de prendre à bras le corps la question des mathématiques, y compris en utilisant des outils de cette méthode, nos observations montrent à quel point c’est un ensemble de facteurs (travail collaboratif des enseignants, engagement contre les fatalités, soutien de la circonscription, aide du PDMQC et du réseau, appui sur des outils mis à leur main, refonte des modalités d’évaluations, attention aux relations avec les familles, différenciation, enseignement explicite…) qui semble contribuer à la réussite d’une école, et non le simple recours à un outil. Ce qui fait la différence, c’est que les professionnels se sentent suffisamment soutenus pour prendre à leur charge leur part de responsabilité, collectivement, pour s’engager."

Pour aller plus loin :

Rémi Brissiaud dans le café pédagogique

De « l’evidence-based practices » aux « practice-based evidences » : et si les chercheurs anglo-saxons nourrissaient des débats éducatifs féconds en France ?

Cette démarche et ces dispositifs sont empruntés à des organisations classiques des classes de mathématiques au primaire (leçon délivrée par l’enseignant, batteries d’exercices déclinés par le maître, critères de validation spécifiques…) mais aussi à des organisations qui le sont moins : les élèves ne font pas tous la même chose en même temps, les erreurs sont développées, écoutées, les formes d’enseignement sont manifestement durables, cohérentes, au long du cursus…

Or nous avons déjà pu souligner ailleurs à quel point la cohérence, la stabilité des pratiques enseignantes au long du cursus, la possibilité de réfléchir et revenir sur ses erreurs, l’absence de stigmatisation de ces erreurs, l’alternance de moments où les contenus travaillés sont identiques pour tous, et de moments où ils sont particuliers à chacun sont des principes essentiels pour des apprentissages efficaces. Il y a donc une part d’innovation et une part de stabilité, dont l’équilibre est à mesurer.

Des changements positifs pour des enseignants jusqu’ici démunis ?

Les enseignants observés et leurs élèves disent « suivre cette méthode » et l’apprécier. C'est en particulier le cas du dossier des « problèmes » donnés aux élèves, avec l’imposition des schémas possibles à utiliser pour chacun de ces problèmes, qui structurent les activités des élèves et des enseignants. Comme ces derniers le disent, « nous avons centré l’enseignement des mathématiques sur la résolution de problèmes ». L’équipe de circonscription, de son côté, enregistre des évolutions de performances manifestes. Comment expliquer que ces enseignants, ces élèves et l’institution éprouvent une telle impression de changements ? et de changements positifs ? Les anciennes pratiques des enseignants les laissaient donc à ce point démunis, insatisfaits de leurs guidages, des aides qu’ils pouvaient apporter à leurs élèves ?

Les « problèmes », exercices emblématiques de la discipline

Le sens du mot « problème » est ici celui des problèmes arithmétiques dont les données numériques sont décimales. L’enseignement des mathématiques (ou du calcul, ou de l’arithmétique) est historiquement fondé sur ces exercices. Les difficultés des élèves à les résoudre sont attestées depuis longtemps et de façon récurrente. Cependant, il est reconnu que l’identification des relations entre les informations numériques que délivre l’énoncé constitue une clé de réussite. Cette identification [de ce qui est appelé « structure du problème » dans ces vidéos] serait favorisée par l’articulation de registres différents : un texte/un schéma/ un tableau/un dessin… (Duval, Flemming-Damm) par l’explicitation, le récit (oral ou écrit) (Julo en particulier). Le maître, pour rendre publique et partagée cette identification peut, dans une classe, demander à chacun d’en inventer une, ou restreindre les choix des élèves en proposant une gamme de possibles représentations (c’est le cas ici), ou encore proposer une activité guidante (Julo).

Dans des classes (que nous avons pu observer ailleurs), des schémas d’aide à la résolution de problèmes sont en effet inventés par les élèves, partagés, testés. Ces aides sont alors mises en concurrence et leur légitimité est celle de leur efficacité perçue. Dans des manuels du siècle dernier figuraient des leçons dans lesquelles des représentations (schématiques, langagières, etc.) efficaces pour la résolution de certains problèmes étaient enseignées. Ces aides, imposées, étaient alors des contenus garantis par le maître. Dans le cas présent, celui de ces vidéos, l’élève doit choisir le « bon schéma » parmi plusieurs imposés : partie/tout, chronologique, comparaison, tableau à 4 cases… Ces schémas sont donc ici des contenus enseignés, garantis par le maître. De plus, ils sont des objets d’évaluations, puisque le choix du « bon » schéma est vérifié et validé (vidéo CE1). Ces contenus disciplinaires sont enfin, toujours dans ces classes, des contenus durables puisqu’enseignés du CP au CM2. Par conséquent, ils ont, pour les élèves, le même statut que d’autres savoirs disciplinaires : choisir, connaître les schémas est sans doute équivalent, en tant que savoir identifié par ces élèves, à poser une division, à identifier le chiffre des dixièmes, etc. Lorsqu’ils ne seront plus des savoirs évalués, redeviendront-ils des aides, et des aides seulement, ou disparaitront-ils, car sans utilité ?

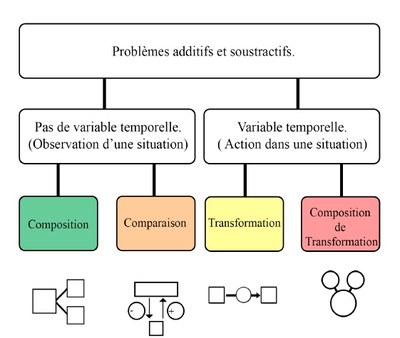Vergnaud-Gueguen Les schémas proposés par le maître M+ correspondent à un classement des énoncés de problèmes : relation partie/tout, comparaison etc. Si les énoncés proposés sont classés, ils sont par conséquent limités par ce classement. Par exemple, il nous semble que ces schémas ne sont pas efficaces dans les problèmes du type (Pierre a 4/5^ème de plus que Paul qui possède 50 euros, etc.) ou des problèmes de dénombrements complexes (combien de rectangles dans cette figure). À ce constat de volontaire délimitation s’ajoute la moindre attention portée à d’autres facteurs de variations entre énoncés de problèmes : les nombres, les mots, les structures des phrases, la longueur des énoncés, l’ordre des informations données etc., dont on connait aussi l’importance (Ehrlirch S. pour exemple). Pour reprendre une des questions soulevées plus haut, est-ce que le choix de différencier les fleurs du bouquet par des noms (tulipes et roses) est le meilleur ? Ne serait-il pas préférable de les différencier, pour cette élève, par des couleurs ? Il ne s’agit pas ici de dénigrer le travail de ces enseignants, qui manifestement réalisent un travail conséquent pour proposer à leurs élèves des énoncés intéressants, mais de poser des questions.

Ces énoncés sont donc composés pour répondre à cette exigence. Ils sont des objets disciplinaires, des discours très particuliers à la discipline mathématique telle qu’elle existe dans ces classes. Nous soulignerons ici deux de ces particularités. Ce sont des énoncés imaginaires (ils ne sont pas construits à partir d’états observés du monde) mais dont les référents sont des états possibles du monde réel. Mais ce sont aussi des descriptions fondées sur le principe d’économie, qui est un principe mathématique. Cela signifie que ces descriptions ne comportent aucune information surabondante, qui pourrait être déduite des autres informations présentes : « j’ai 8 billes, j’en ai gagné 5 » est un énoncé qui obéit à ce principe, « j’avais 3 billes, j’en ai gagné 5, j’en ai 8 » est un énoncé qui n’y obéit pas. La question que nous pouvons nous poser, est celle du statut de ces particularités : sont-elles des connaissances dans la classe ? Des contenus disciplinaires, au même titre que les différents schémas ? Il ne nous semble pas que ce soit le cas, car ces particularités ne sont pas enseignées, ne sont pas évaluées. Par conséquent reste à savoir si les maîtres et les élèves, qui font l’expérience de ces particularités, mais qui ne la disent ou ne la formalisent sans doute pas, considèrent ces particularités comme des aides, des entraves ou encore les pensent sans importance ou involontaires. (à remettre toujours en question, observées une fois mais sans plus).

Les temporalités

Ingrid-horloge Les rythmes des classes, tels que les vidéos nous les laissent découvrir diffèrent selon les enseignants, selon les dispositions de la classe – en groupe, seul, en classe entière -, et selon les contenus. Par exemple, la relation entre le rythme (imposé ici par l’enseignante Ingrid) et le contenu en jeu peut s’étudier dans la vidéo (Ingrid) :

L’enseignante annonce la tâche, avec un ton égal ; activité de comptage de 5 en 5, rythme saccadé, 5/10/15, doigt pointé sur les chiffres de l’horloge ; annonce de l’enseignante, ton ascendant (alerte ! - on « sait lire » 3h 40, on « va lire » 3h moins 20-) ; activité de comptage dans le sens contraire 5/10/15, doigt pointé sur les chiffres de l’horloge.

Ces rythmes différents distinguent deux contenus : lire l’heure dans les deux sens, direct et indirect, et maîtriser le comptage de 5 en 5. Le côté théâtral de la scansion laisse ou autorise à supposer que les élèves et l’enseignante reconnaissent le comptage comme savoir structurant et la lecture de l’heure comme savoir structuré.Mais les temporalités ne sont pas réduites aux rythmes. Nous pouvons être attentifs aussi aux durées, aux ruptures de rythmes en quelque sorte. Des accélérations soudaines sont des entrées pour saisir l’incompréhension temporaire des élèves.

Dans la vidéo (Marianne en résolution de problèmes) le M+ prend un temps conséquent pour représenter la situation (porte-monnaie, robes, prix…), et engager la discussion. « Peux-tu en prendre une ? deux ? ». En revanche, le temps s’accélère tout à coup lorsque la question de l’opération à choisir est posée « alors, quelle opération ? une multiplication ou une division ? ». Fallait-il suspendre encore le temps à ce moment-là, pour cet élève-là ?

Enfin, pour conclure, l’entrée par les temporalités permet aussi de souligner à quel point les échanges peuvent être longs, soutenus, dans ces classes (ce qui rompt avec des pratiques habituelles en classe de mathématiques) et de s’intéresser, au contraire, aux silences de certains. De quoi sont-ils la marque (comme dans la vidéo d'Ingrid) ?

Navigation