Les références théoriques mobilisées
Ce que cela demande de mobiliser des références théoriques
 « Pour nous, formateurs REP+, passer de la lecture d’un article scientifique à la conception d’un parcours de formation, n’a pas été simple. L’article de Raymond Duval est plutôt ardu à lire et à comprendre, mais il est venu mettre les mots que nous cherchions pour mettre au jour ce que voulait dire “comprendre un énoncé de problème”. Alors que nous construisions parallèlement un parcours de formation sur la compréhension des textes littéraires avec les démarches “Pas à pas”Centre Alain-Savary (2018). Séance d'enseignement : Lecture pas-à-pas. https://centre-alain-savary.ens-lyon.fr/CAS/thematiques/LECTURE-ECRITURE/pp-comprehension/scenarios-de-formation/copy2_of_letude-de-la-langue-au-service-de-la-comprehension-scenario-de-formationet “Visibiléo”Centre Alain-Savary (2018). Séance d'enseignement : Le visibiléo. https://centre-alain-savary.ens-lyon.fr/CAS/thematiques/LECTURE-ECRITURE/pp-comprehension/scenarios-de-formation/letude-de-la-langue-au-service-de-la-comprehension-scenario-de-formation. qui visent à enseigner la compréhension des implicites des textes et permettent de visualiser les liens logiques d’une histoire, se pouvait-il que les énoncés de problèmes soient un type de texte spécifique qui possède sa propre logique et des implicites qu’il s’agirait d’aider les élèves à mettre au jour ?
« Pour nous, formateurs REP+, passer de la lecture d’un article scientifique à la conception d’un parcours de formation, n’a pas été simple. L’article de Raymond Duval est plutôt ardu à lire et à comprendre, mais il est venu mettre les mots que nous cherchions pour mettre au jour ce que voulait dire “comprendre un énoncé de problème”. Alors que nous construisions parallèlement un parcours de formation sur la compréhension des textes littéraires avec les démarches “Pas à pas”Centre Alain-Savary (2018). Séance d'enseignement : Lecture pas-à-pas. https://centre-alain-savary.ens-lyon.fr/CAS/thematiques/LECTURE-ECRITURE/pp-comprehension/scenarios-de-formation/copy2_of_letude-de-la-langue-au-service-de-la-comprehension-scenario-de-formationet “Visibiléo”Centre Alain-Savary (2018). Séance d'enseignement : Le visibiléo. https://centre-alain-savary.ens-lyon.fr/CAS/thematiques/LECTURE-ECRITURE/pp-comprehension/scenarios-de-formation/letude-de-la-langue-au-service-de-la-comprehension-scenario-de-formation. qui visent à enseigner la compréhension des implicites des textes et permettent de visualiser les liens logiques d’une histoire, se pouvait-il que les énoncés de problèmes soient un type de texte spécifique qui possède sa propre logique et des implicites qu’il s’agirait d’aider les élèves à mettre au jour ?
Le déclic s’est fait pour nous à la lecture de ce passage de l’article "décrire, visualiser ou raisonner : quels 'apprentissages premiers' de l'activité mathématique ? R.Duval (2003). Décrire, visualiser ou raisonner : quels "apprentissages premiers" de l'activité mathématique ? Annales de didactique et sciences cognitives, volume 8.p.13-62.https://mathinfo.unistra.fr/websites/math-info/irem/Publications/Annales_didactique/vol_08/adsc8-2003_001.pdf de Raymond Duval :
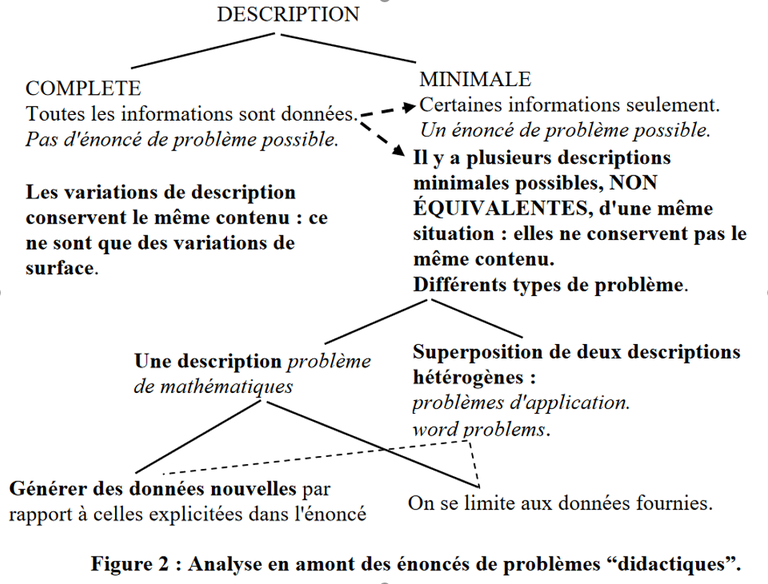
“On peut ainsi donner une définition procédurale d'un énoncé de problème : on obtient un énoncé de problème EN AMPUTANT LA DESCRIPTION COMPLÈTE d'une situation et, cognitivement, il y a autant de types d'énoncés différents qu'il y a de manières différentes de supprimer des données dans une description complète pour obtenir UNE DESCRIPTION MINIMALE, (c'est-à-dire une description permettant de reconstituer la description complète.) Autrement dit, l'énoncé change d'abord en fonction des données supprimées.”
Raymond Duval (2003, ibid p.22)
 On a beau être enseignant depuis des années, avoir donné des centaines de problèmes à résoudre aux élèves, ce qu’est un problème est transparent pour nous et il faut les mots du didacticien pour voir cette évidence : un problème est une description amputée. Mais R. Duval continue :
On a beau être enseignant depuis des années, avoir donné des centaines de problèmes à résoudre aux élèves, ce qu’est un problème est transparent pour nous et il faut les mots du didacticien pour voir cette évidence : un problème est une description amputée. Mais R. Duval continue :
" Un problème a la spécificité de superposer deux descriptions différentes, l’une explicite qui décrit une situation avec des mots, l’autre, implicite, qui est la structure mathématique des relations entre les données numériques de l’énoncé induite par les mots : “[...] ce que l'on appelle les “informations pertinentes” de l'énoncé, celles que l'élève doit “sélectionner”, correspondent chacune au CROISEMENT DE DEUX DÉTERMINATIONS SÉMANTIQUES DIFFÉRENTES. C'est la prise en compte du croisement de deux déterminations sémantiques différentes qui permet de repérer une information et c'est cette prise en compte qui différencie radicalement la lecture d'un énoncé mathématique et celle d'un énoncé ordinaire !”
Raymond Duval (2003, ibid p.26)
 Comprendre un énoncé de problème serait donc comprendre la description mathématique induite par une description verbale qui “habille” avec une situation concrète cette description mathématique, c’est donc le “déshabiller” pour mettre au jour le problème mathématique sous-jacent. Mais comment apprendre aux élèves à comprendre cela ? Dans son article, R. Duval, fait cette proposition didactique :
Comprendre un énoncé de problème serait donc comprendre la description mathématique induite par une description verbale qui “habille” avec une situation concrète cette description mathématique, c’est donc le “déshabiller” pour mettre au jour le problème mathématique sous-jacent. Mais comment apprendre aux élèves à comprendre cela ? Dans son article, R. Duval, fait cette proposition didactique :
“Pour faire entrer les élèves dans la dynamique, très particulière, du questionnement générant les problèmes mathématiques de nature “didactique”, il est nécessaire de les faire d'abord travailler sur la description complète d'une situation et ensuite de leur faire inventorier les différentes manières d'amputer cette description complète pour obtenir des descriptions minimales. Cela relève de ce que nous avons appelé une analyse en amont, et non pas en aval, des problèmes (Duval, 2002 p. 98-100.) Naturellement le critère d'une description minimale consiste dans la possibilité de retrouver la donnée supprimée à partir des données conservées : cela implique donc que l'on analyse aussi les opérations permettant de passer d'une donnée à une autre. Autrement dit, c'est en travaillant sur le passage d'une description complète à une description minimale possible d'un objet ou d'une situation que les élèves peuvent entrer dans la compréhension d'un énoncé de problème. Sans un tel travail, les énoncés de problèmes, c'est-à-dire des descriptions minimales particulières, restent une activité aveugle et aléatoire pour la grande majorité des élèves. Et, finalement, la résolution d'un problème reste aussi idiosyncrasique, aussi fragmentaire que le remplissage d'une grille de mots croisés. Il suffit de changer un mot pour que tout à nouveau s'embrouille “dans la tête”.”
Raymond Duval (2003, ibid p.31)
 Cette proposition nous a semblé particulièrement intéressante pour améliorer la compréhension des énoncés par nos élèves de REP+, mais il fallait pour cela concevoir une formation qui permette aux enseignants d’en faire quelque chose…»
Cette proposition nous a semblé particulièrement intéressante pour améliorer la compréhension des énoncés par nos élèves de REP+, mais il fallait pour cela concevoir une formation qui permette aux enseignants d’en faire quelque chose…»
Et si la compréhension des énoncés cachait des problèmes de description ?
 Les formateurs ont sollicité le centre Alain-Savary pour documenter la question de la résolution de problème et ses dimensions langagières en particulier sur une approche sémantique des énoncés verbaux des problèmes en mathématiques. Ces dimensions ont donné lieu à de nombreuses ressources sur le site du centre Alain Savary Rubrique "mathématique" du centre Alain Savary., néanmoins cette question reste vive pour les professionnels et les problèmes à énoncés verbaux construits par et pour l’école restent des objets de formation très complexes à appréhender.
Les formateurs ont sollicité le centre Alain-Savary pour documenter la question de la résolution de problème et ses dimensions langagières en particulier sur une approche sémantique des énoncés verbaux des problèmes en mathématiques. Ces dimensions ont donné lieu à de nombreuses ressources sur le site du centre Alain Savary Rubrique "mathématique" du centre Alain Savary., néanmoins cette question reste vive pour les professionnels et les problèmes à énoncés verbaux construits par et pour l’école restent des objets de formation très complexes à appréhender.
" La question des rapports entre apprentissage et résolution de problèmes est sans doute l’une des plus complexes qui se pose dans le domaine des recherches sur l’enseignement "
Jean Julo (2002)J.Julo (2002), des apprentissages spécifiques pour la résolution de problème ? IREM de Grenoble. https://irem.univ-grenoble-alpes.fr/medias/fichier/69n4_1555591199676-pdf.
 L’article “Décrire, visualiser ou raisonner : Quels 'apprentissages premiers' de l'activité mathématique ?“ cité par les formateurs a permis d’aborder la question avec une autre approche. L’énoncé de problème (“word problem”) devient un objet d’étude, et la focale porte sur l’importance de la description en mathématiques, très souvent invisibilisée et pourtant centrale dans une démarche scientifique.
L’article “Décrire, visualiser ou raisonner : Quels 'apprentissages premiers' de l'activité mathématique ?“ cité par les formateurs a permis d’aborder la question avec une autre approche. L’énoncé de problème (“word problem”) devient un objet d’étude, et la focale porte sur l’importance de la description en mathématiques, très souvent invisibilisée et pourtant centrale dans une démarche scientifique.
" L'observation des phénomènes, l'enregistrement de données nouvelles et leur description joue un rôle primordial dans le travail scientifique. Car les connaissances dépendent d'abord de l'extension du champ des observations qui peuvent être effectuées et du degré de leur discrimination. En insistant sur les “conceptions”, les “explications”, leur “validation”, l'enseignement des sciences ne tend-il pas sous-estimer le temps et l'importance du travail d'observation et de description nécessaire pour l'apprentissage ? "
Raymond Duval (2003, ibid p.14)
Description complète et descriptions minimales
|
Description complète et minimale
Registres de représentation sémiotiques Les registres de représentations sémiotiques sont des notions issues des travaux de R.Duval. Ils ont fait l’objet d’une ressource sur le site et sont mobilisés pour lire une activité de résolution de problème mathématique conjointe d'une enseignante et d'élèves en 5e. Lien sur le site. |
 Le didacticien montre que tous les énoncés verbaux ont pour caractéristique d’être des descriptions complètes de phénomènes “amputés” de certaines données qu’il faut reconstituer (par exemple chercher le nombre de billes gagnées par une personne à l'aide d'un calcul). Ainsi il souligne l'importance des tâches de description dans l'apprentissage en mathématiques. D’après l’auteur, non seulement ces tâches de description permettent une activité fondamentale en sciences, base de toutes connaissances, mais consistent également à provoquer une activité de représentation qui implique la mobilisation d'un ou plusieurs registres sémiotiques et qui dépend de leur maîtrise par les élèves (par exemple l’usage d’un schéma pour signifier la structure du problème ou des chiffres pour écrire les nombres).
Le didacticien montre que tous les énoncés verbaux ont pour caractéristique d’être des descriptions complètes de phénomènes “amputés” de certaines données qu’il faut reconstituer (par exemple chercher le nombre de billes gagnées par une personne à l'aide d'un calcul). Ainsi il souligne l'importance des tâches de description dans l'apprentissage en mathématiques. D’après l’auteur, non seulement ces tâches de description permettent une activité fondamentale en sciences, base de toutes connaissances, mais consistent également à provoquer une activité de représentation qui implique la mobilisation d'un ou plusieurs registres sémiotiques et qui dépend de leur maîtrise par les élèves (par exemple l’usage d’un schéma pour signifier la structure du problème ou des chiffres pour écrire les nombres).
Une autre caractéristique commune aux énoncés verbaux est la superposition de deux descriptions hétérogènes : d'une part celle d'un traitement "instancié" et d'autre part une description de la situation “concrète” pour “donner du sens”.
Par exemple : 8 =3+5 est une description complète à traitement "instancié". On peut lui associer une description complète “concrète” qui lui est hétérogène : “ Cet après-midi Aïcha a huit billes. Elle en avait trois ce matin et elle en a gagné cinq” ou “Un bouquet de huit fleurs est composé de trois tulipes et cinq roses”. Ces deux dernières descriptions sont non équivalentes (l'une est une "transformation" et l'autre est une "composition" au sens des schèmes de G.Vergnaud)
Élaborer des descriptions minimales à partir d'une description complète
 Sur un exemple, les descriptions complètes "concrètes" de 8=3+5 permettent d'élaborer des descriptions dites minimales en "amputant" une donnée.
Sur un exemple, les descriptions complètes "concrètes" de 8=3+5 permettent d'élaborer des descriptions dites minimales en "amputant" une donnée.
En "amputant" la donnée 8 on peut écrire la description minimale suivante : “Aïcha avait trois billes, elle en gagne cinq, combien en a-t-elle maintenant ?” ou celle-ci "Il y a trois tulipes et cinq roses, combien y a-t-il de fleurs ? " en "amputant" la donnée 3 on obtient une autre description minimale : “Aïcha avait huit billes, elle a perdu cinq billes, combien lui en reste-t-il maintenant ? “ ou celle-ci " Cet après-midi Aïcha a huit billes, elle en a gagné cinq ce matin, combien en avait-elle avant de jouer ?"
Le didacticien attire l’attention sur le fait que l’expression “résolution de problème “ est trop globalisante du fait d’une très grande diversité des tâches. Il y a d’autres types de problèmes :
- qui nécessitent de générer de nouvelles données (par exemple “ Trouver toutes les décompositions additives en nombres entiers du nombre huit”)
- quand les données sont toutes présentes dans l’énoncé (par exemple : “Vérifier que la somme de trois et cinq est huit”)
Ce travail de codage sémantique est utile pour mieux maîtriser le recodage sémantique, notion mobilisée par le cognitiviste Emmanuel Sander qui instruit le rôle des analogies dans la résolution de problèmes aux cycles 2 et 3 et qui sont de trois types : substitution, scénario ou simulationE.Sander (2019). Le rôle des analogies dans la résolution de problèmes aux cycles 2 et 3. https://centre-alain-savary.ens-lyon.fr/CAS/thematiques/mathematiques-en-education-prioritaire/compte-rendus-formations-de-formateurs-mathematiques/session-2019-2020/le-role-des-analogies-intuitives-dans-la-resolution-de-problemes-arithmetiques-aux-cycles-2-et-3.. D'après le cognitiviste, le recodage sémantique, conduit par l'enseignant, consiste à faire avancer la compréhension d’un élève en allant à l’encontre de son intuition. Parfois des éléments de la situation orientent vers une certaine conception mathématique, mais celle-ci n’est pas adaptée au problème. Le recodage sémantique va initier une autre façon de percevoir le problème, qui, elle, est cohérente avec les objectifs mathématiques visés.
Axe paradigmatique et axe syntagmatique
|
Extrait du dictionnaire de linguistique
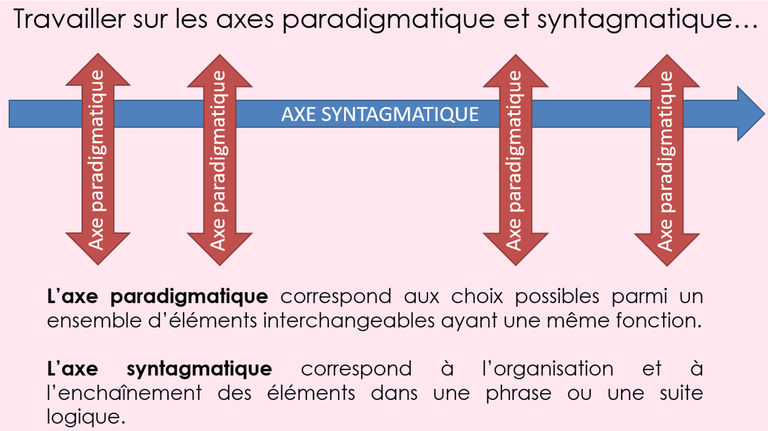
L'entrée "Axe" dans le dictionnaire Les linguistes [...] ont pris l'habitude d'opposer l'axe syntagmatique (axe horizontal des rapports entretenus par les unités dans la chaîne parlée) et l'axe paradigmatique (axe vertical des rapports virtuels entretenus par les unités susceptibles de commuter). Extrait de la conférence chapitrée d'Anne Sardier "Former à l'enseignement-apprentissage du lexique : discussion lexicale et réemploi " |
 « Nous leur avons proposé aussi un schéma présentant les notions issues de la linguistique structurale (voir l’entrée axe dans le dictionnaire de linguistique de Jean Dubois, p.61) d’axe paradigmatique et d’axe syntagmatique, afin de montrer que dans un énoncé de problème, on peut faire varier l’axe paradigmatique sans que le problème mathématique induit ne change.
« Nous leur avons proposé aussi un schéma présentant les notions issues de la linguistique structurale (voir l’entrée axe dans le dictionnaire de linguistique de Jean Dubois, p.61) d’axe paradigmatique et d’axe syntagmatique, afin de montrer que dans un énoncé de problème, on peut faire varier l’axe paradigmatique sans que le problème mathématique induit ne change.
Par exemple on peut varier certaines unités de l'axe paradigmatique de cet énoncé : “ Cet après-midi Aïcha a huit billes. Elle en avait trois ce matin et elle en a gagné cinq” en remplaçant les "billes" par des "cartes" ce qui donne ce nouvel énoncé : “ Cet après-midi Aïcha a huit cartes. Elle en avait trois ce matin et elle en a gagné cinq” , qui n'est pas équivalent du point de vue sémantique mais qui est strictement identique du point de vue de la description mathématique.
Une double transposition didactique : De la recherche à la formation, de la formation à la classe
 Contrairement à certaines idées reçues sur l’application de solutions “toutes faites” issues de la recherche dans les classes, notre travail a nécessité une “traduction” de la théorie et de la proposition didactique d’un chercheur, pour permettre son appropriation par les enseignants en formation. Mais cela a aussi nécessité une “traduction” aux équipes et à chaque enseignant pour concevoir et mener une séquence de classe utile aux élèves pour mieux comprendre les énoncés de problèmes :
Contrairement à certaines idées reçues sur l’application de solutions “toutes faites” issues de la recherche dans les classes, notre travail a nécessité une “traduction” de la théorie et de la proposition didactique d’un chercheur, pour permettre son appropriation par les enseignants en formation. Mais cela a aussi nécessité une “traduction” aux équipes et à chaque enseignant pour concevoir et mener une séquence de classe utile aux élèves pour mieux comprendre les énoncés de problèmes :
- Choix pédagogiques et didactiques
- Remobilisation de gestes professionnels et d’outils préexistants au service de cette démarche, de son utilité et de son utilisabilité pour les élèves.
D’où l’importance dans ce processus de formation du dernier temps qui ramène le réel de la classe, les choix de chacun, avec ce qu’ils permettent de gagner, mais aussi ce qu’ils font perdre. Comme pour toute démarche, c’est dans les détails de la mise en œuvre que se joue l’efficacité. »